1.3 Meson
this section introduce Yukawa’s original theory about meson
![notes on 1.3 Meson [part1]](https://physics.run/wp-content/uploads/2023/01/WCM0049.png)
![notes on 1.3 Meson [part2]](https://physics.run/wp-content/uploads/2023/01/WCM0050.png)
1.3 Meson
this section introduce Yukawa’s original theory about meson
![notes on 1.3 Meson [part1]](https://physics.run/wp-content/uploads/2023/01/WCM0049.png)
![notes on 1.3 Meson [part2]](https://physics.run/wp-content/uploads/2023/01/WCM0050.png)
Loading Wolfram cloud notebook need s few seconds, take a break maybe?
Copyright of the code belongs to the owner of this site, the codes are completely open-source, use it as you like.
Derive relativistic structure equation (TOV equation) from static spherically symmetric spacetime
prerequisites: GR at the level of Schutz’s textbook or track1 of MTW
0.1.1 Metric of Static Spherically Symmetric Stars
The metric of spherically symmetric spacetime is:
$$
\mathrm{d} s^2=g_{00} \mathrm{~d} t^2+2 g_{0 r} \mathrm{~d} r \mathrm{~d} t+g_{r r} \mathrm{~d} r^2+r^2 \mathrm{~d} \Omega^2
\tag{1.1}$$
We define a static spacetime to be one in which we can find a time coordinate $t$ with two properties: (i) all metric components are independent of $t$, and (ii) the geometry is unchanged by time reversal, $t \rightarrow-t$. (A spacetime with property (i) but not necessarily (ii) is said to be stationary.)
Condition (ii) has the following implication. The coordinate transformation $(t, r, \theta, \phi) \rightarrow$ $(-t, r, \theta, \phi)$ has $\Lambda^{\overline{0}}{ }_0=-1, \Lambda_j^i=\delta_j^i$, and we find:
$$
\left.g_{\bar{0} \bar{0}}=\left(\Lambda^0_{\bar{0}}\right)^2g_{00}=g_{00} \right.\
$$
$$
g_{\bar{0} \bar{r}}=\Lambda_{\bar{0}}^0 \Lambda^r_{\bar{r}} g_{0 r}=-g_{0 r}\
$$
$$
g_{\bar{r} \bar{r}}=\left(\Lambda^r {\bar{r}}\right)^2 g{r r}=g_{r r}
\tag{1.2}$$
by assuming $g_{00}<0$ and $g_{rr}>0$ $($ we shall see these conditions do hold inside stars $)$, denote: $g_{00}=-e^{2\phi}$ and $g_{rr}=e^{2\lambda}$
then solve Eq.$(1.2)$ for the metric of static spherically symmetric spacetime:
$$
\mathrm{d} s^2=-\mathrm{e}^{2 \Phi} \mathrm{d} t^2+\mathrm{e}^{2 \Lambda} \mathrm{d} r^2+r^2 d \Omega^2
\tag{1.3}$$
0.1.2 Einstein Tensors
We can show that for the metric given by Eq. $(1.3)$, the Einstein tensor has components:
$$
\begin{aligned}
&G_{00}=\frac{1}{r^2} \mathrm{e}^{2 \Phi} \frac{\mathrm{d}}{\mathrm{d} r}\left[r\left(1-\mathrm{e}^{-2 \Lambda}\right)\right] \\
&G_{r r}=-\frac{1}{r^2} \mathrm{e}^{2 \Lambda}\left(1-\mathrm{e}^{-2 \Lambda}\right)+\frac{2}{r} \Phi^{\prime} \\
&G_{\theta \theta}=r^2 \mathrm{e}^{-2 \Lambda}\left[\Phi^{\prime \prime}+\left(\Phi^{\prime}\right)^2+\Phi^{\prime} / r-\Phi^{\prime} \Lambda^{\prime}-\Lambda^{\prime} / r\right] \\
&G_{\phi \phi}=\sin ^2 \theta G_{\theta \theta}
\end{aligned}
\tag{1.4}$$
where $\Phi^{\prime}:=\mathrm{d} \Phi / \mathrm{d} r$, etc. All other components vanish.
0.1.3 Structure Equations
In this subsection we derive Tolman-Oppenheimer-Volkof equation from the $r$ component of conservation law along with the $(r,r)$ component of \textit{Einstein field equation}, and then an auxiliary equation from the $(t,t)$ component of Einstein field equation, and end with an introduction on the equation of state EoS
The stress-energy tensor of perfect fluid is given by:
$$
T^{\alpha \beta}=(\rho+p) U^\alpha U^\beta+p \eta^{\alpha \beta}
\tag{1.5}$$
alongs with the conservation law: $T^{\alpha \beta}_{; \beta}=0$, of which the $r$ component gives:
$$
(\rho+p) \frac{\mathrm{d} \Phi}{\mathrm{d} r}=-\frac{d p}{\mathrm{~d} r}
\tag{1.6}$$
Einstein field equation states: $G^{\alpha \beta}=8 \pi T^{\alpha \beta}$, by denoting: $m(r):=\frac{1}{2} r\left(1-\mathrm{e}^{-2 \Lambda}\right)$ and substitute Einstein tensors by eq$(1.4)$, the $(r,r)$ component of field equation reads:
$$
\frac{\mathrm{d} \Phi}{\mathrm{d} r}=\frac{m(r)+4 \pi r^3 p}{r[r-2 m(r)]}
\tag{1.7}$$
Now by combing Eq$(1.6)$ and Eq$(1.7)$, we can eliminate $\Phi$ and obtain:
$$
\frac{\mathrm{d} p}{\mathrm{~d} r}=-\frac{(\rho+p)\left(m+4 \pi r^3 p\right)}{r(r-2 m)}
\tag{1.8}$$
known as the \textbf{\textit{Tolman-Oppenheimer-Volkov equation}}
In addition to Eq$(1.7)$, the $(t,t)$ component of Einstein field equation gives another structure equation:
$$
\frac{\mathrm{d} m(r)}{\mathrm{d} r}=4 \pi r^2 \rho
\tag{1.9}$$ where again we have denoted $g_{rr}$ by $\left(1-\frac{2 m(r)}{r}\right)^{-1}$.
To complete the struction equations requires a relation between energy density $\rho$ and pressure $p$, called the Equation of State (EoS):
$$
\rho = \rho(p)
\tag{1.10}$$
0.1.4 Boundary Conditions and General Solving Procedure
To solve for $m(r)$ and $p(r)$ from TOV equation Eq$(1.8)$ and auxiliary equation Eq$(1.9)$ along with EoS Eq$(1.10)$, we need two boundary conditions:
The first boundary on $m$ given by properties of spacetime, we state without a proof$($check Schutz if you want$)$:
$$
m(r=0)=0
\tag{1.11}$$
while the second arbitrarily chosen:
$$
p(r=0)=p_c
\tag{1.12}$$
STEP1: with these two boundary conditions providing two integral constants, we can obtain expressions for $m=m(r)$ and $p=p(r)$ simply by integration
STEP2: with condition $p(R)=0$ and expression obtained in STEP1, obtaining $R$; then obtain $M$ by $M=m(R)$
STEP3: to solve for $\Phi(r)$ from Eq$(1.6)$, which need another boundary condition on $\phi$, this can be obtained from continuity condition and Schwarzschild exterior metric which yields $g_{00}(r=R)=-\left(1-\frac{2 M}{R}\right)$, substitute $M$ and $R$ gives the boundary condition on $g_{00}(r=0)$, or equivalently, $\Phi(r=0)$
STEP4: the final step is to solve for $\Phi(r)$ from conservation law Eq$(1.6$ with boundary condition from STEP3
1.2 Photon
solution of Compton scattering may also serve as an exercise of relativity


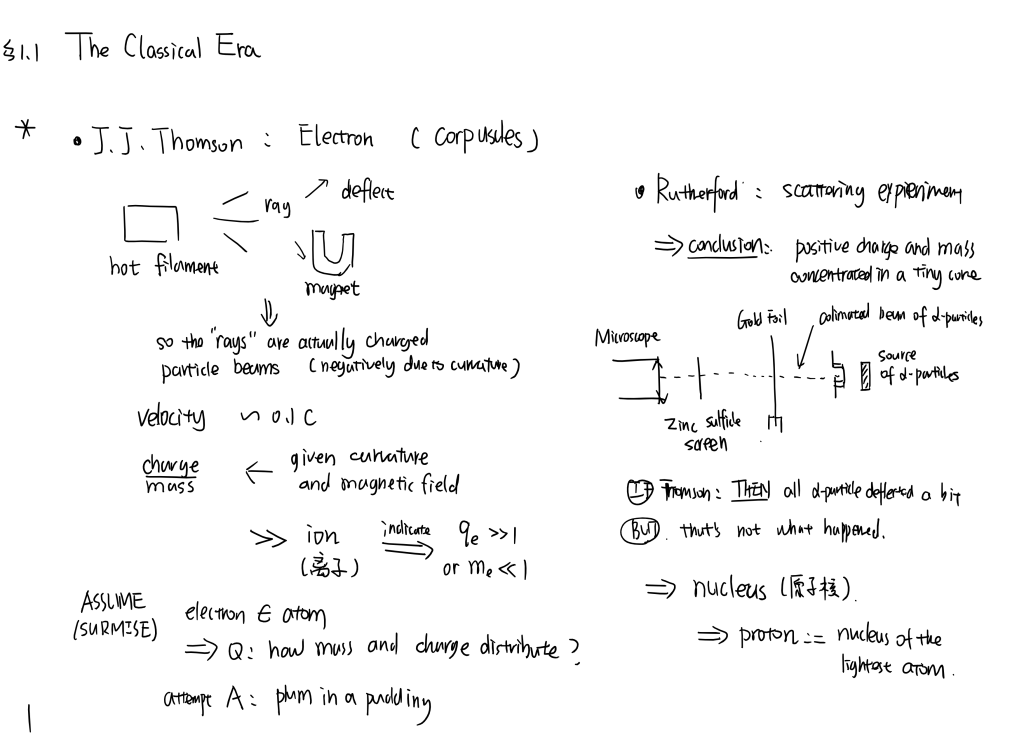
1.1 the Electrical Era
from J. J. Thomson’s discovery of electron to Bohr’s model of hydrogen

This is an introduction to Griffiths’s classical textbook of Elementary Particles
What is matter made of?
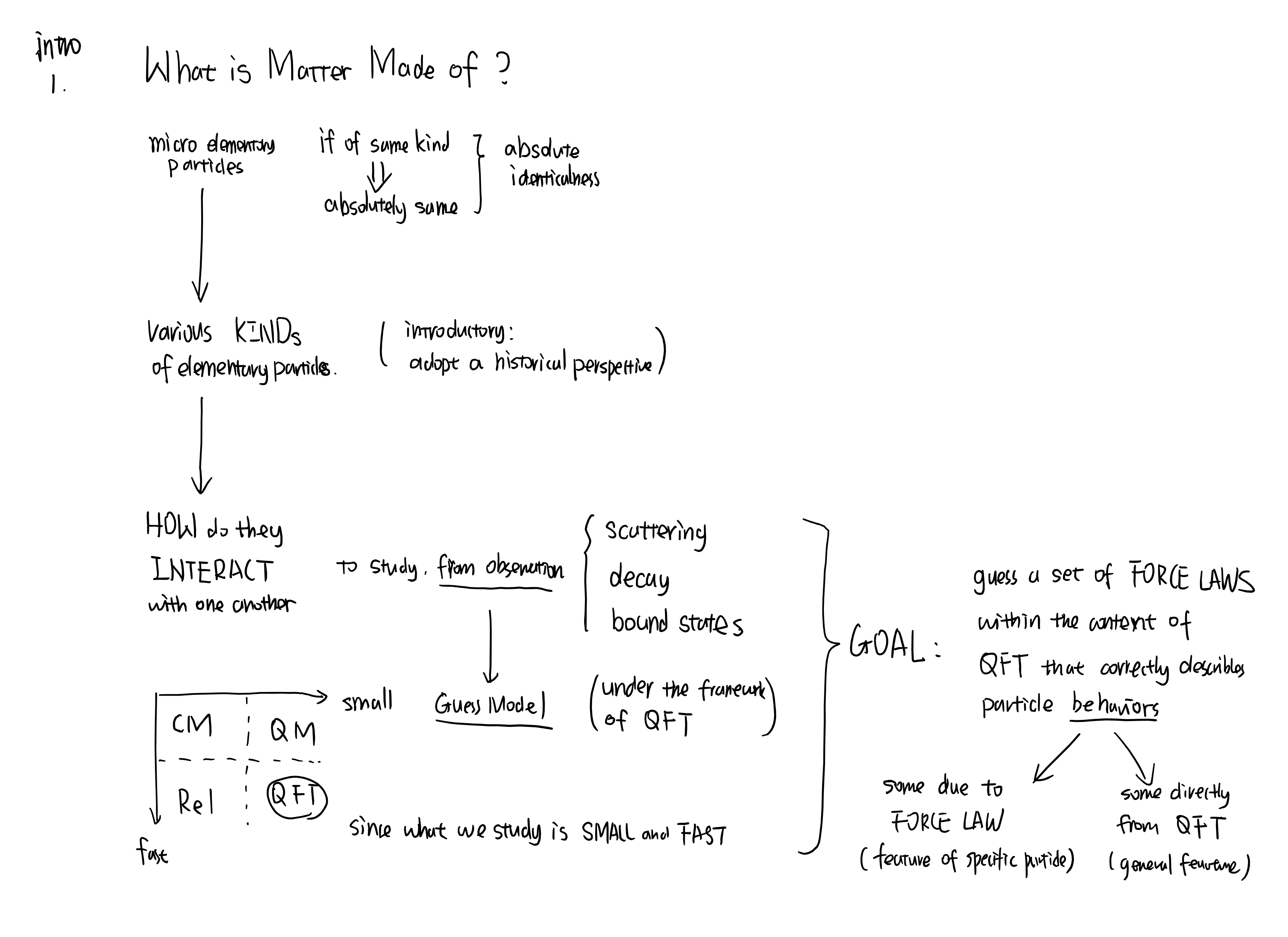
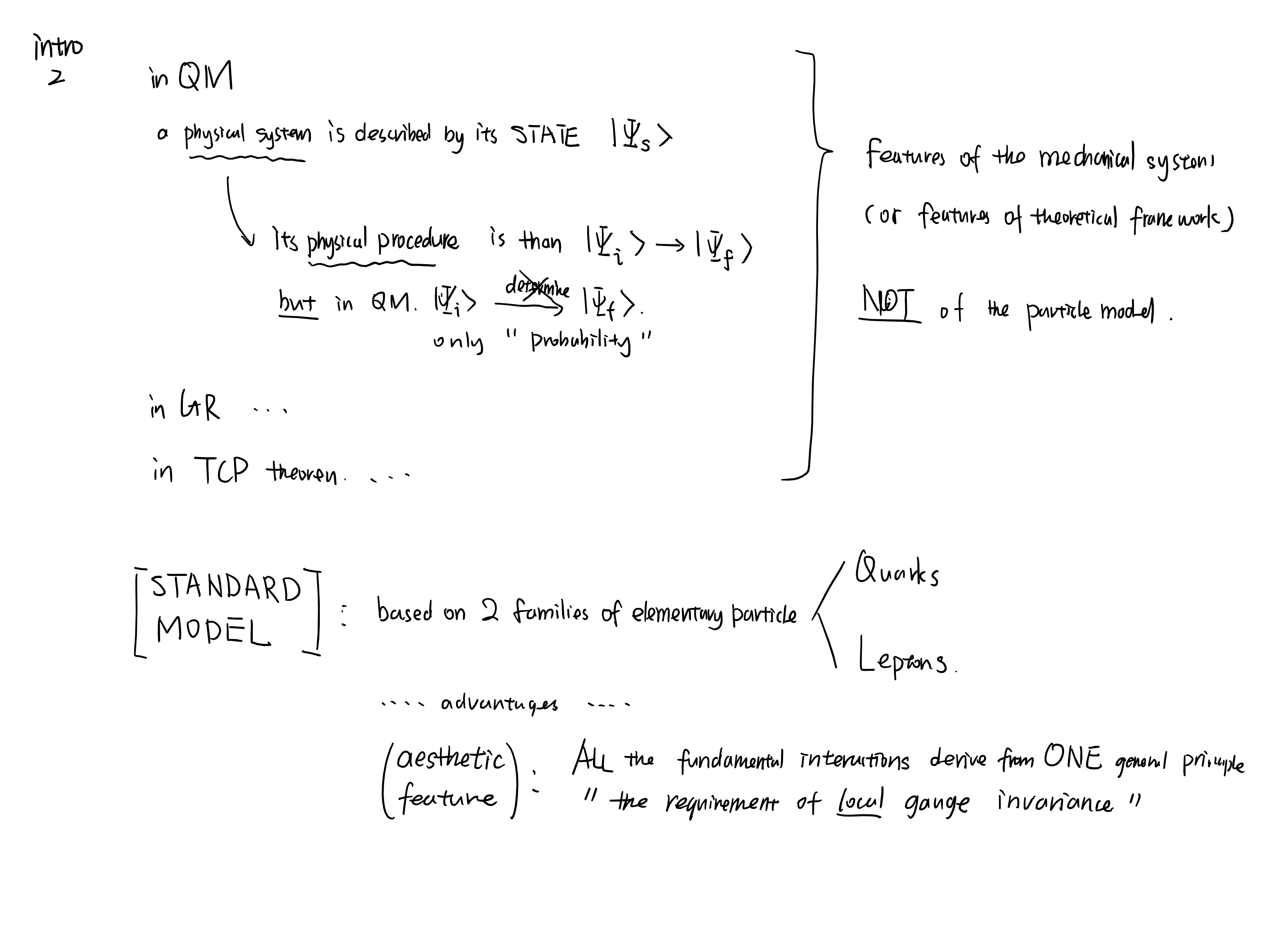
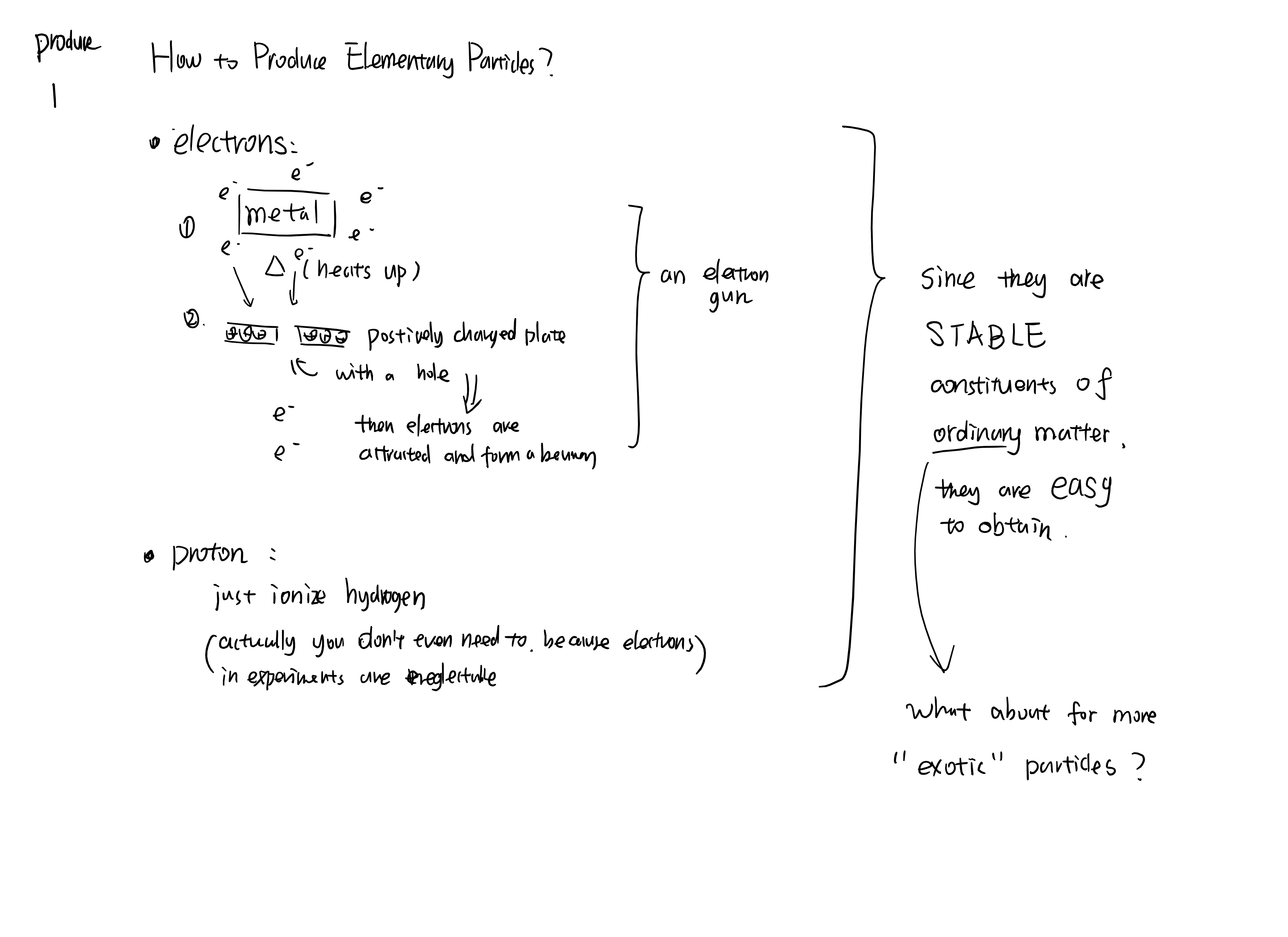
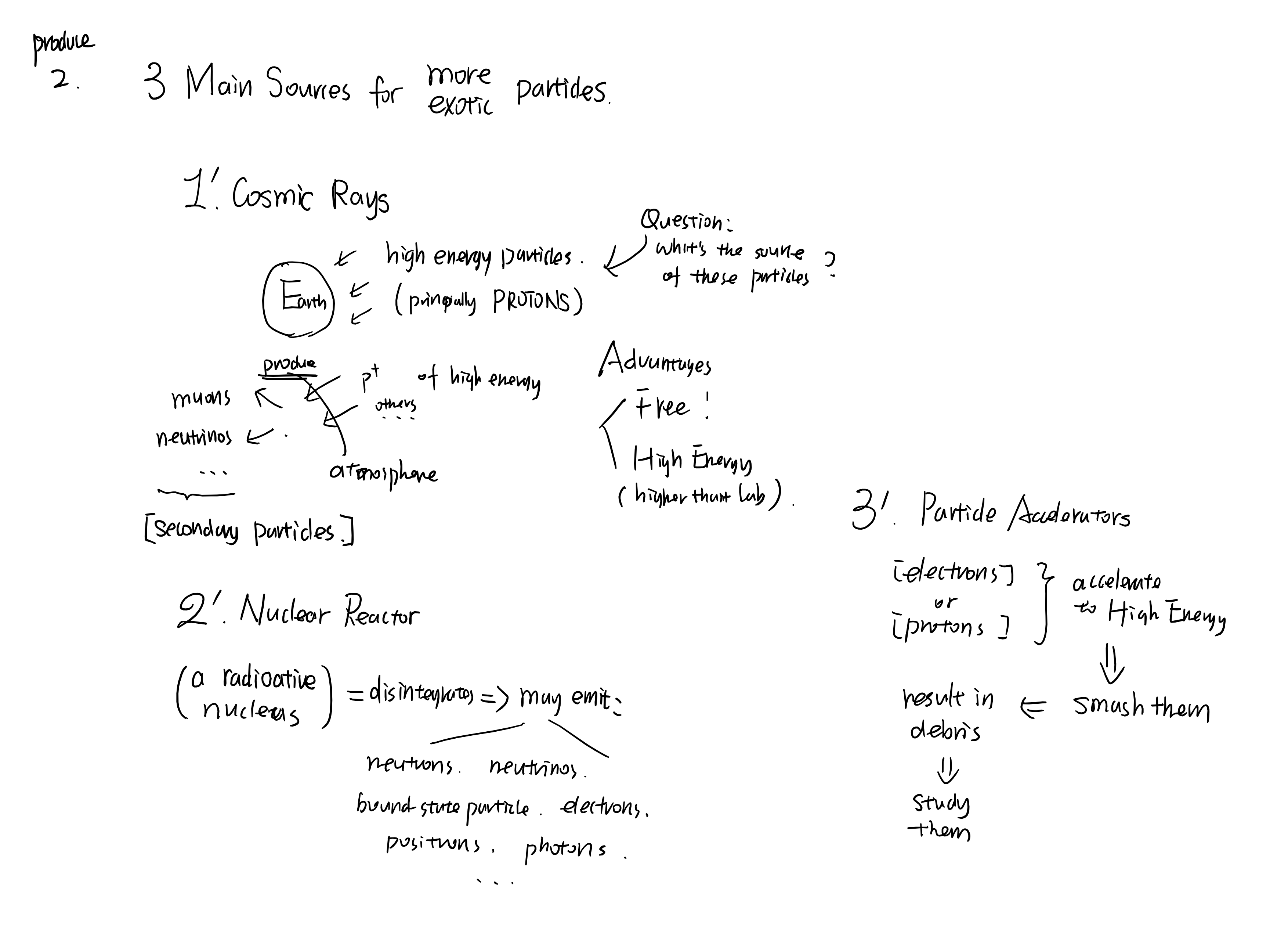
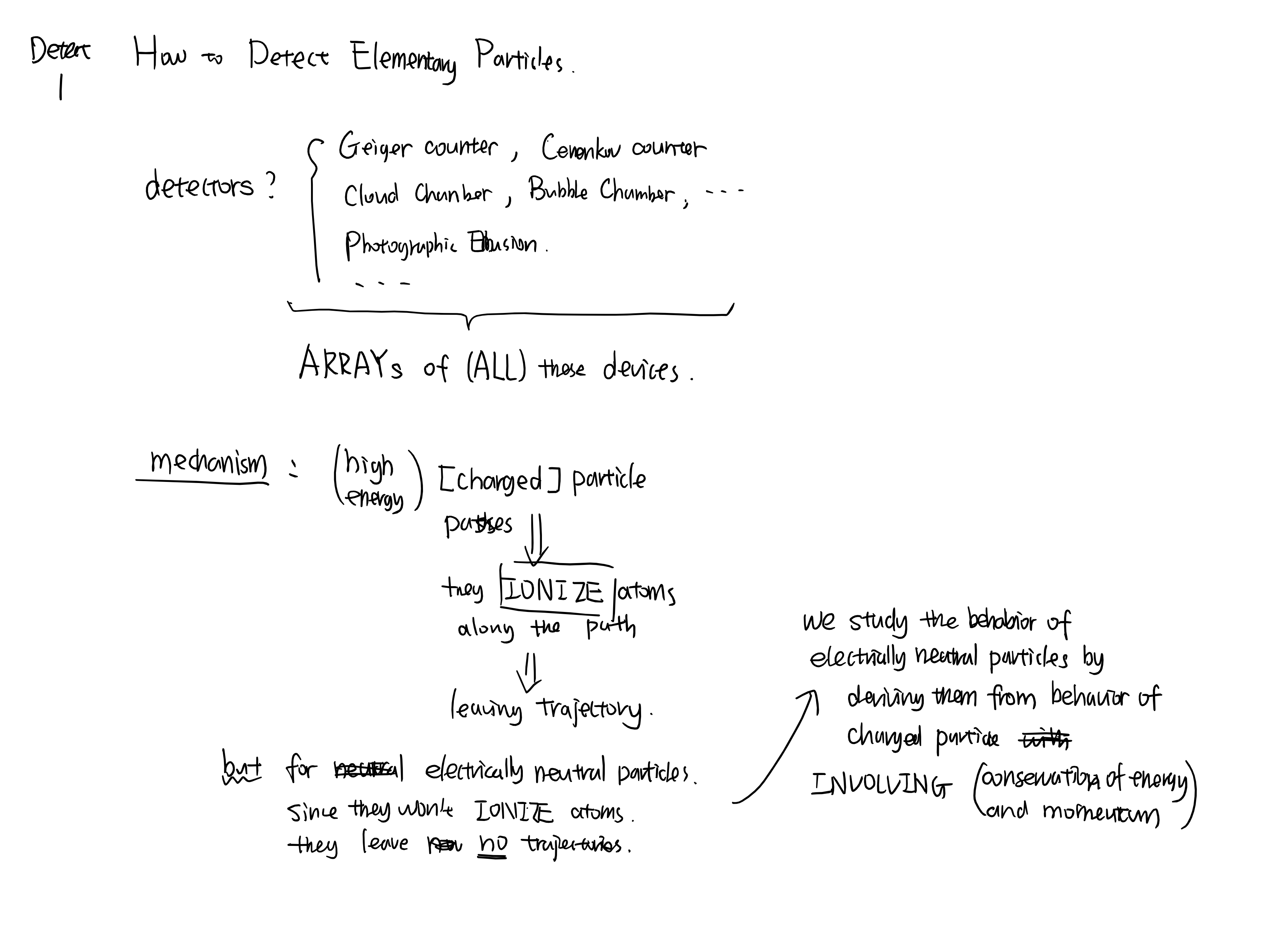

This note can be use as an example of tensor analysis
This article shows the derivation of Newtonian tidal effect from Newton’s equation of motion and gravity, with the notation of tensor analysis and Einstein summation convention. This may serve as an example for beginners in tensor analysis to check their comprehension, meanwhile as a baby version or lead-in to geodesic deviation of general relativity.
Newton’s second law (componentwise)
$$
\frac{d^{2} x^{i}}{d t^{2}} \equiv a^{i} \equiv \frac{F^{i}}{m}
$$
Newtonian equation of gravitation
$$
\frac{F^{i}}{m}=-\eta^{i j} \partial_{j} \phi
$$
combine two equations give:
$$
\frac{d^{2} x^{i}}{d t^{2}}=-\eta i j\left[\partial_{j} \phi\right]_{\vec{x}}
$$
where the subscription $\vec{x}$ denotes the derivative is operated at position $\vec{x}$ similarly we have at $\vec{x}+\vec{n}$ :
$$
\frac{d^{2}\left(x^{i}+n^{i}\right)}{d t^{2}}=-\eta^{i j}\left[\partial_{j} \phi\right]_{\vec{x}+\vec{n}}
$$
make subtraction give:
$$
\frac{d^{2} n^{i}}{d t^{2}}=-\eta^{i j}\left(\left[\partial_{j} \phi\right]{\vec{x}+\vec{n}}-\left[\partial{j} \phi\right]_{\vec{x}}\right)
$$
given $\vec{n}$ is infinitesimal, we have RHS:
$$
\text { RHS }=-\eta^{i j} n^{k}\left[\partial_{k}\left(\partial_{j} \phi\right)\right]_{\vec{x}}
$$
set Cartesian coordinates originated from centre of earth orient the $z$-axis so that is consists with $\vec{x}$ (position vector) then $\vec{X}=\left(X^{1}, X^{2}, X^{3}\right)=(0,0, z)$.
gravitational potential is given by:
$$
\phi=-\frac{G M}{r}=-\frac{G M}{\left(x^{2}+y^{2}+z^{2}\right)^{1 / 2}}
$$
and thus
$$
\begin{aligned}
\partial_{j} \phi & =\frac{\partial \phi}{\partial x^{j}} \\
& =-\frac{d \phi}{d r} \frac{\partial r}{\partial x^{j}} \\
& =\frac{G M}{r^{3}} x^{j}
\end{aligned}
$$
and
$$
\begin{aligned}
\partial_{k} \partial_{j} \phi & =\frac{\partial}{\partial x^{k}}\left(\frac{G M}{r^{3}} x^{j}\right) \\
& =\frac{\partial}{\partial x^{k}}\left(\frac{G M}{r^{3}}\right) x^{j}+\delta_{k}^{j} \frac{G M}{r^{3}} \\
& =-\frac{3 G M}{r^{4}} x^{j}+\delta_{k}^{j} \frac{G M}{r^{3}}
\end{aligned}
$$
thus.
$$
\begin{aligned}
& \frac{d^{2}}{d t^{2}} n^{x}=-\frac{G M}{r^{3}} n^{x} \\
& \frac{d^{2}}{d t^{2}} n^{y}=-\frac{G M}{r^{3}} n^{y} \\
& \frac{d^{2}}{d t^{2}} n^{z}=\frac{2 G M}{r^{3}} n^{z}
\end{aligned}
$$
This article is rearranged based on Qianye YU’s previous work, Physics Reserved Labour is fully authorized to make the reprint.
qyggtql
Lagrangian of free rigid body in its comoving reference frame is given by:
$$
L=\sum_{i} \frac{1}{2} I_{i} \omega_{i}^{2}
$$
where angular velocities can be expressed in Eulerian angles: $\omega_{1}=\dot{\varphi} \sin \theta \sin \psi+$ $\dot{\theta} \cos \psi, \omega_{2}=\dot{\varphi} \sin \theta \cos \psi-\dot{\theta} \sin \psi, \omega_{3}=\dot{\varphi} \cos \theta+\dot{\psi}$.
Substitute into EL equations:
$$
\frac{d}{d t}\left(\frac{\partial \mathcal{L}}{\partial \dot{q}_{i}}\right)=\frac{\partial \mathcal{L}}{\partial q_{i}}
$$
where $q_{i}$ take $q_{1}=\theta, q_{2}=\varphi, q_{3}=\psi$.
Apply chain rule to both sides of (2) :
$$
\begin{aligned}
\frac{\partial \mathcal{L}}{\partial q_{i}} & =\sum_{j=1}^{3} \frac{\partial \mathcal{L}}{\partial \omega_{j}} \frac{\partial \omega_{j}}{\partial q_{i}} \\
\frac{\partial \mathcal{L}}{\partial \dot{q}_{i}} & =\sum_{j=1}^{3} \frac{\partial \mathcal{L}}{\partial \omega_{j}} \frac{\partial \omega_{j}}{\partial \dot{q}_{i}}
\end{aligned}
$$
Substitute $q_{3}$ by $\psi$ in (2), RHS:
$$
\begin{aligned}
\frac{\partial \mathcal{L}}{\partial \psi} & =\sum_{i=1}^{3} \frac{\partial \mathcal{L}}{\partial \omega_{i}} \frac{\partial \omega_{i}}{\partial \psi} \\
& =\sum_{i=1}^{3} I_{i} \omega_{i} \frac{\partial \omega_{i}}{\partial \psi} \\
& =I_{1} \omega_{1}(\dot{\varphi} \sin \theta \cos \psi-\dot{\theta} \sin \psi)+I_{2} \omega_{2}(-\dot{\varphi} \sin \theta \sin \psi-\dot{\theta} \cos \psi)+0 \\
& =I_{1} \omega_{1} \omega_{2}+I_{2} \omega_{2}\left(-\omega_{1}\right) \\
& =\left(I_{1}-I_{2}\right) \omega_{1} \omega_{2}
\end{aligned}
$$
*this note is rearranged based on Qianye YU’s work LHS:
$$
\frac{d}{d t}\left(\frac{\partial \mathcal{L}}{\partial \dot{\psi}}\right)=I_{3} \dot{\omega}_{3}
$$
Combing (2)(4)(5) gives the first Euler dynamic equation:
$$
\left(I_{1}-I_{2}\right) \omega_{1} \omega_{2}-I_{3} \dot{\omega}_{3}=0
$$
Similarly substitute $q_{2}$ by $\varphi$ into equation(2). Since $\frac{\partial \mathcal{L}}{\partial \varphi}=0$, we have:
$$
\frac{d}{d t}\left(\frac{\partial \mathcal{L}}{\partial \dot{\varphi}}\right)=0
$$
Apply chain rule to LHS of (7) gives:
$$
\begin{aligned}
0= & I_{1} \dot{\omega}_{1} \sin \theta \sin \psi+I_{2} \dot{\omega}_{2} \sin \theta \cos \psi+I_{3} \dot{\omega}_{3} \cos \theta+I_{1} \omega_{1}(\cos \theta \sin \psi \dot{\theta} \\
& +\sin \theta \cos \psi \dot{\psi})+I_{2} \omega_{2}(\cos \theta \cos \psi \dot{\theta}-\sin \theta \sin \psi \dot{\psi})-I_{3} \omega_{3} \sin \theta \dot{\theta}
\end{aligned}
$$
We introduce $A=I_{1} \omega_{1}(\cos \theta \sin \psi \dot{\theta}+\sin \theta \cos \psi \dot{\psi})$ and $B=I_{2} \omega_{2}(\cos \theta \cos \psi \dot{\theta}-$ $\sin \theta \sin \psi \dot{\psi})$ to reduce the calculation.
Notice $I_{3} \dot{\omega}_{3}=\left(I_{1}-I_{2}\right) \omega_{1} \omega_{2}$. So (8) is equivalent to:
$$
\begin{aligned}
\sin \theta\left[I_{1} \dot{\omega}_{1} \sin \psi+I_{2} \dot{\omega}_{2} \cos \psi\right] & =\left(I_{2}-I_{1}\right) \omega_{1} \omega_{2} \cos \theta+I_{3} \omega_{3} \sin \theta \dot{\theta}-A-B \\
& =I_{1}\left(-\omega_{1} \omega_{2} \cos \theta-\omega_{1} \cos \theta \sin \psi \dot{\theta}-\omega_{1} \sin \theta \cos \psi \dot{\psi}\right) \\
& +I_{2}\left(\omega_{1} \omega_{2} \cos \theta-\omega_{2} \cos \theta \cos \psi \dot{\theta}+\omega_{2} \sin \theta \sin \psi \dot{\psi}\right) \\
& +I_{3} \omega_{3} \sin \theta \dot{\theta} \\
& =I_{1} \omega_{1}(-\dot{\varphi} \sin \theta \cos \psi \cos \theta+\dot{\theta} \sin \psi \cos \theta-\dot{\theta} \sin \psi \cos \theta-\sin \theta \cos \psi \dot{\psi}) \\
& +I_{2} \omega_{2}(\dot{\varphi} \sin \theta \sin \psi \cos \theta+\dot{\theta} \cos \psi \cos \theta-\dot{\theta} \cos \psi \cos \theta+\sin \theta \sin \psi \dot{\psi}) \\
& +I_{3} \omega_{3} \sin \theta \dot{\theta} \\
& =I_{1} \omega_{1}(-\dot{\varphi} \sin \theta \cos \psi \cos \theta-\sin \theta \cos \psi \dot{\psi}) \\
& +I_{2} \omega_{2}(\dot{\varphi} \sin \theta \sin \psi \cos \theta+\sin \theta \sin \psi \dot{\psi}) \\
& +I_{3} \omega_{3} \sin \theta \dot{\theta}
\end{aligned}
$$
Dividing (9) through $\sin \theta$ gives:
$$
\begin{aligned}
I_{1} \dot{\omega}_{1} \sin \psi+I_{2} \dot{\omega}_{2} \cos \psi & =I_{1} \omega_{1}(-\dot{\varphi} \cos \psi \cos \theta-\cos \psi \dot{\psi}) \\
& +I_{2} \omega_{2}(\dot{\varphi} \sin \psi \cos \theta+\sin \psi \dot{\psi}) \\
& +I_{3} \omega_{3} \dot{\theta}
\end{aligned}
$$
We keep equation (10) for later use
Substituting $q_{3}$ by $\theta$ into equation $(2)$ :
$$
\frac{d}{d t}\left(\frac{\partial \mathcal{L}}{\partial \dot{\theta}}\right)=\frac{\partial \mathcal{L}}{\partial \theta}
$$
So,
$$
\begin{aligned}
\frac{d}{d t}\left(I_{1} \omega_{1} \cos \psi-I_{2} \omega_{2} \sin \psi\right)= & I_{1} \omega_{1} \dot{\varphi} \cos \theta \sin \psi+I_{2} \omega_{2} \dot{\varphi} \cos \theta \cos \psi \\
& +I_{3} \omega_{3} \dot{\varphi}(-\sin \theta)
\end{aligned}
$$
which gives:
$$
\begin{aligned}
I_{1} \dot{\omega}_{1} \cos \psi-I_{2} \dot{\omega}_{2} \sin \psi= & I_{1} \omega_{1}(\dot{\varphi} \cos \theta \sin \psi+\sin \psi \dot{\psi}) \\
& +I_{2} \omega_{2}(\dot{\varphi} \cos \theta \cos \psi+\cos \psi \dot{\psi}) \\
& -I_{3} \omega_{3} \dot{\varphi} \sin \theta
\end{aligned}
$$
Since (10) and (13) are obtained from EL equation of generalized coordinates $\varphi$ and $\theta$ respectively, along with (6), we have used all three independent EL equations, the other two Euler equations must be obtained directly from combinations of (10) and (13):
Firstly, (10) $\cdot \sin \psi+(13) \cdot \cos \psi$ gives:
$$
\begin{aligned}
I_{1} \dot{\omega}_{1} & =I_{2} \omega_{2}(\dot{\varphi} \cos \theta+\dot{\psi})+I_{3} \omega_{3}(\dot{\theta} \sin \psi-\dot{\varphi} \sin \theta \cos \psi) \\
& =I_{2} \omega_{2} \omega_{3}+I_{3} \omega_{3}\left(-\omega_{2}\right) \\
& =\left(I_{2}-I_{3}\right) \omega_{2} \omega_{3}
\end{aligned}
$$
And $(10) \cdot \cos \psi-(13) \cdot \sin \psi$ gives:
$$
\begin{aligned}
I_{2} \dot{\omega}_{2} & =I_{1} \omega_{1}(-\dot{\varphi} \cos \theta-\dot{\psi})+I_{3} \omega_{3}(\dot{\theta} \cos \psi+\dot{\varphi} \sin \theta \sin \psi) \\
& =I_{1} \omega_{1}\left(-\omega_{3}\right)+I_{3} \omega_{3} \omega_{1} \\
& =\left(I_{3}-I_{1}\right) \omega_{3} \omega_{1}
\end{aligned}
$$
Rearranging (6),(14),(15) gives the Eulerian dynamic equations:
$$
\left\{\begin{array}{l}
\left(I_{1}-I_{2}\right) \omega_{1} \omega_{2}-I_{3} \dot{\omega}_{3}=0 \\
\left(I_{2}-I_{3}\right) \omega_{2} \omega_{3}-I_{1} \dot{\omega}_{1}=0 \\
\left(I_{3}-I_{1}\right) \omega_{3} \omega_{1}-I_{2} \dot{\omega}_{2}=0
\end{array}\right.
$$
Welcome to WordPress. This is your first post. Edit or delete it, then start writing!