1.2 Photon
康普顿散射的计算可以作为相对论的入门习题


1.2 Photon
康普顿散射的计算可以作为相对论的入门习题


本文是格里菲斯大神Introduction to Elementary Particles一书简介部分的笔记
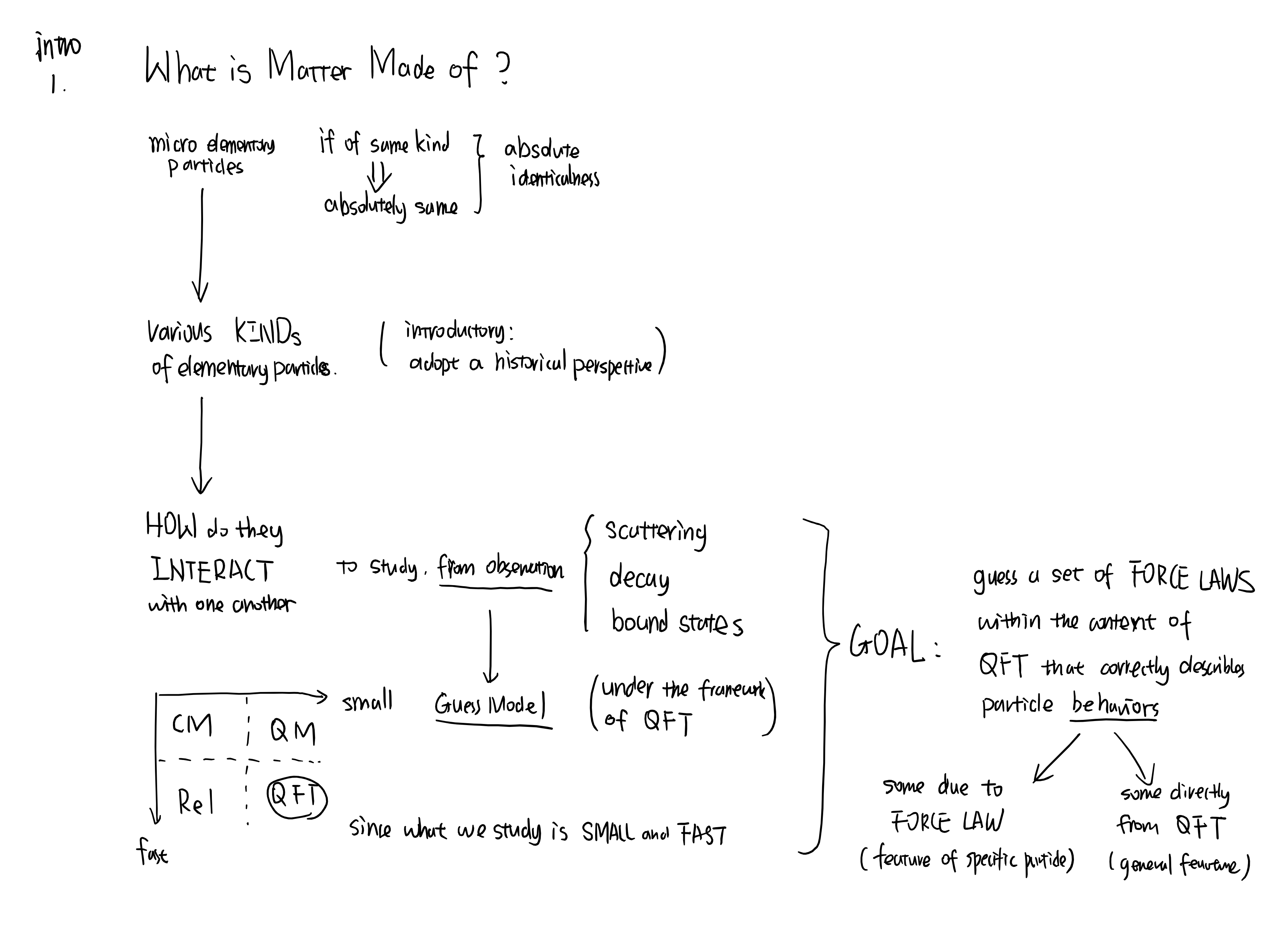
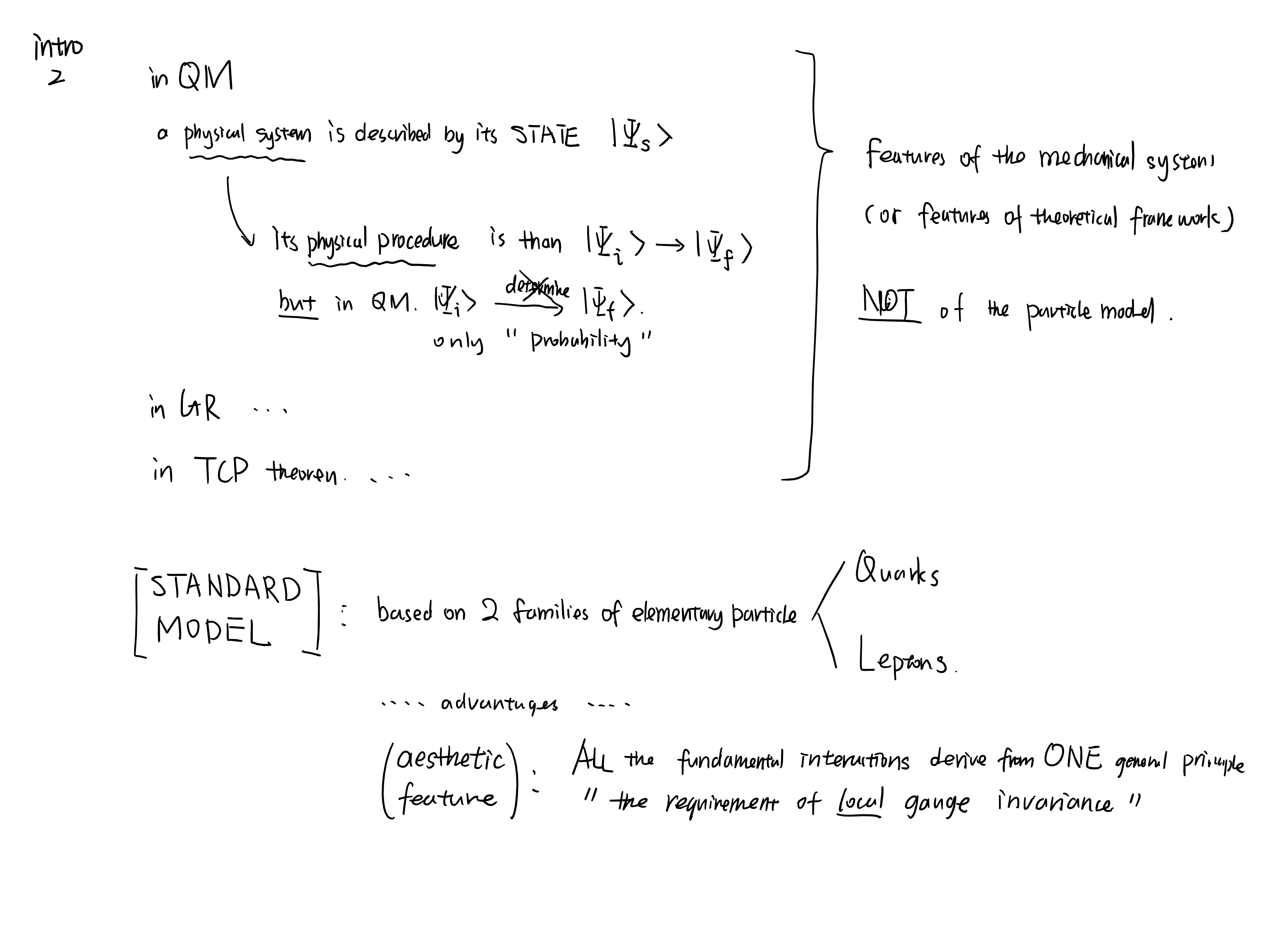
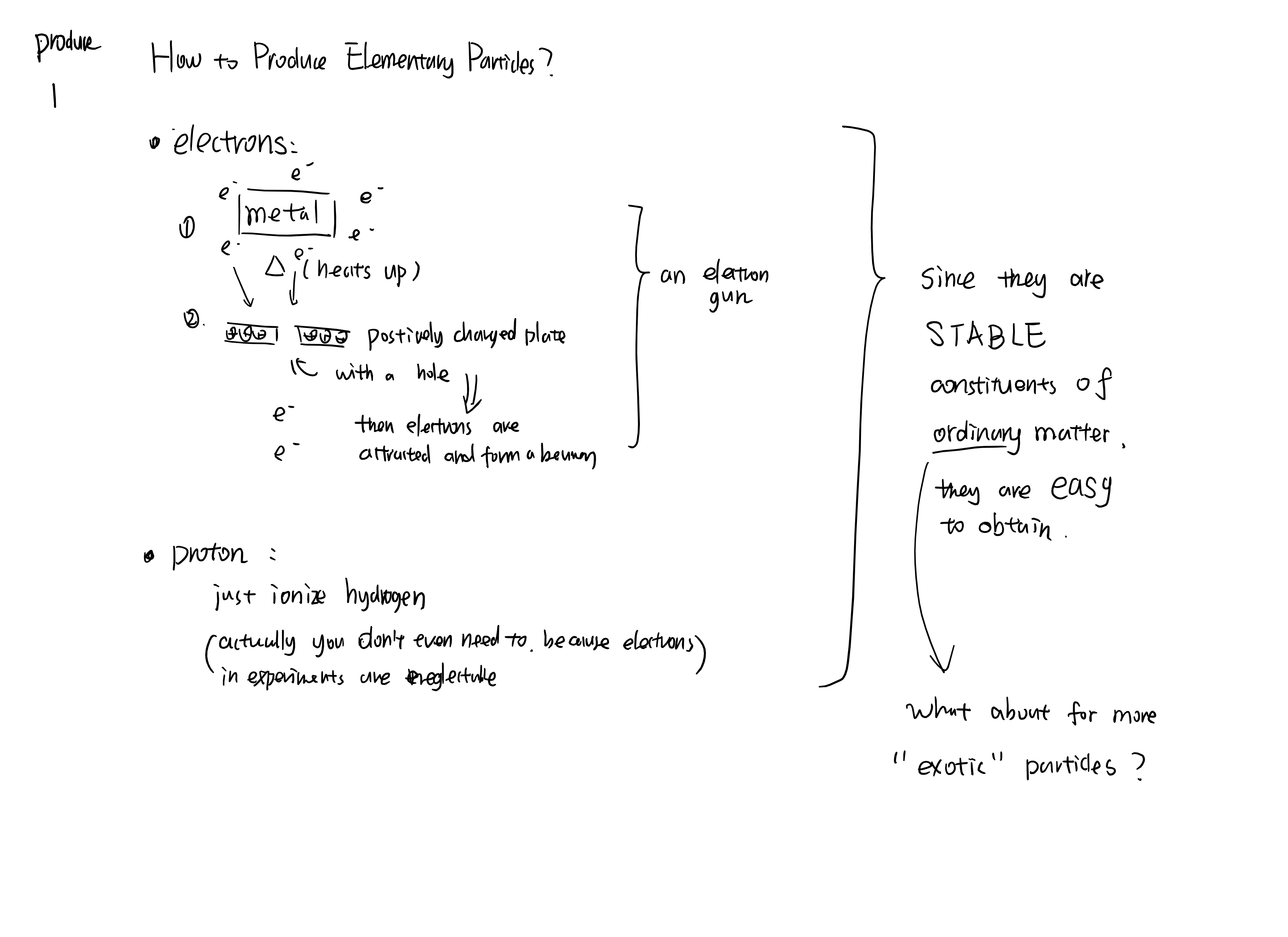
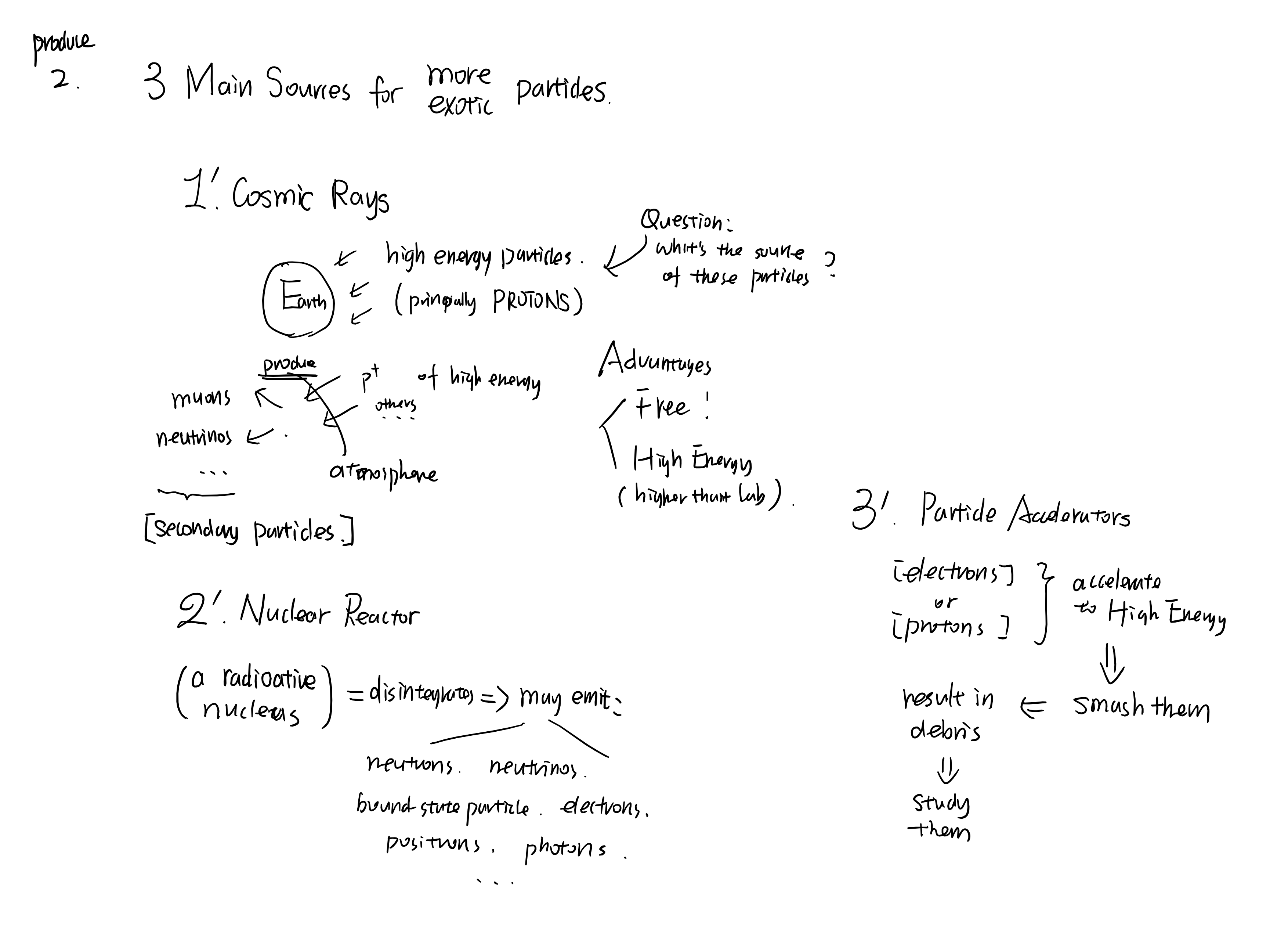
物质是如何构成的
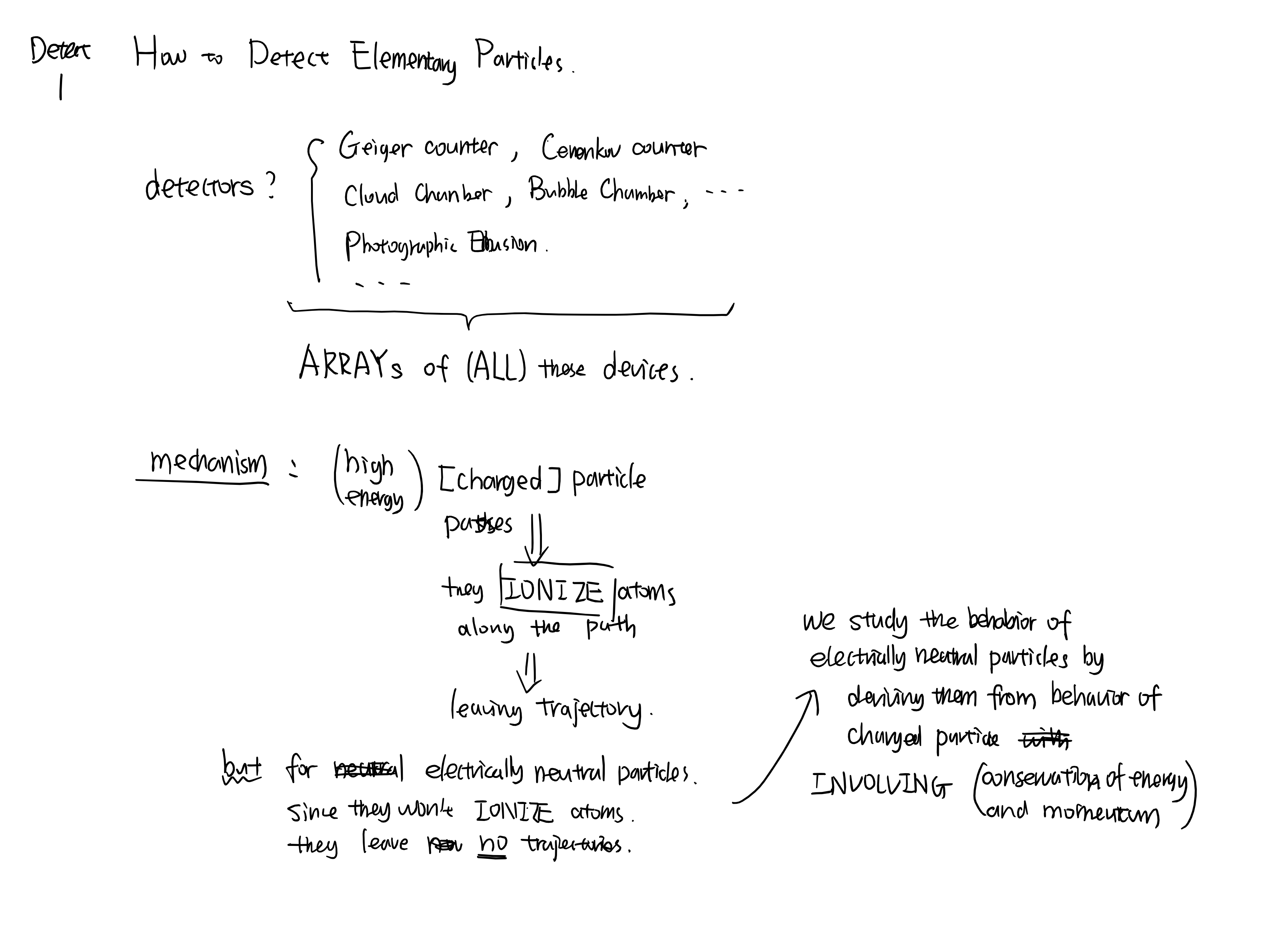

本文适合作为张量分析自学入门的一个案例
从牛顿引力和运动学公式出发,利用张量语言推到和描述经典力学框架下的潮汐效应,张量分析的初学者可以此为例联系基本计算和对方向导数的理解,同时作为广义相对论中测地线偏离理论的先导
Newton’s second law (componentwise)
$$
\frac{d^{2} x^{i}}{d t^{2}} \equiv a^{i} \equiv \frac{F^{i}}{m}
$$
Newtonian equation of gravitation
$$
\frac{F^{i}}{m}=-\eta^{i j} \partial_{j} \phi
$$
combine two equations give:
$$
\frac{d^{2} x^{i}}{d t^{2}}=-\eta i j\left[\partial_{j} \phi\right]_{\vec{x}}
$$
where the subscription $\vec{x}$ denotes the derivative is operated at position $\vec{x}$ similarly we have at $\vec{x}+\vec{n}$ :
$$
\frac{d^{2}\left(x^{i}+n^{i}\right)}{d t^{2}}=-\eta^{i j}\left[\partial_{j} \phi\right]_{\vec{x}+\vec{n}}
$$
make subtraction give:
$$
\frac{d^{2} n^{i}}{d t^{2}}=-\eta^{i j}\left(\left[\partial_{j} \phi\right]{\vec{x}+\vec{n}}-\left[\partial{j} \phi\right]_{\vec{x}}\right)
$$
given $\vec{n}$ is infinitesimal, we have RHS:
$$
\text { RHS }=-\eta^{i j} n^{k}\left[\partial_{k}\left(\partial_{j} \phi\right)\right]_{\vec{x}}
$$
set Cartesian coordinates originated from centre of earth orient the $z$-axis so that is consists with $\vec{x}$ (position vector) then $\vec{X}=\left(X^{1}, X^{2}, X^{3}\right)=(0,0, z)$.
gravitational potential is given by:
$$
\phi=-\frac{G M}{r}=-\frac{G M}{\left(x^{2}+y^{2}+z^{2}\right)^{1 / 2}}
$$
and thus
$$
\begin{aligned}
\partial_{j} \phi & =\frac{\partial \phi}{\partial x^{j}} \\
& =-\frac{d \phi}{d r} \frac{\partial r}{\partial x^{j}} \\
& =\frac{G M}{r^{3}} x^{j}
\end{aligned}
$$
and
$$
\begin{aligned}
\partial_{k} \partial_{j} \phi & =\frac{\partial}{\partial x^{k}}\left(\frac{G M}{r^{3}} x^{j}\right) \\
& =\frac{\partial}{\partial x^{k}}\left(\frac{G M}{r^{3}}\right) x^{j}+\delta_{k}^{j} \frac{G M}{r^{3}} \\
& =-\frac{3 G M}{r^{4}} x^{j}+\delta_{k}^{j} \frac{G M}{r^{3}}
\end{aligned}
$$
thus.
$$
\begin{aligned}
& \frac{d^{2}}{d t^{2}} n^{x}=-\frac{G M}{r^{3}} n^{x} \\
& \frac{d^{2}}{d t^{2}} n^{y}=-\frac{G M}{r^{3}} n^{y} \\
& \frac{d^{2}}{d t^{2}} n^{z}=\frac{2 G M}{r^{3}} n^{z}
\end{aligned}
$$
本文整理自俞千野同学的工作,预备役物理民工经授权搬运
千野哥哥太强了
Lagrangian of free rigid body in its comoving reference frame is given by:
$$
L=\sum_{i} \frac{1}{2} I_{i} \omega_{i}^{2}
$$
where angular velocities can be expressed in Eulerian angles: $\omega_{1}=\dot{\varphi} \sin \theta \sin \psi+$ $\dot{\theta} \cos \psi, \omega_{2}=\dot{\varphi} \sin \theta \cos \psi-\dot{\theta} \sin \psi, \omega_{3}=\dot{\varphi} \cos \theta+\dot{\psi}$.
Substitute into EL equations:
$$
\frac{d}{d t}\left(\frac{\partial \mathcal{L}}{\partial \dot{q}_{i}}\right)=\frac{\partial \mathcal{L}}{\partial q_{i}}
$$
where $q_{i}$ take $q_{1}=\theta, q_{2}=\varphi, q_{3}=\psi$.
Apply chain rule to both sides of (2) :
$$
\begin{aligned}
\frac{\partial \mathcal{L}}{\partial q_{i}} & =\sum_{j=1}^{3} \frac{\partial \mathcal{L}}{\partial \omega_{j}} \frac{\partial \omega_{j}}{\partial q_{i}} \\
\frac{\partial \mathcal{L}}{\partial \dot{q}_{i}} & =\sum_{j=1}^{3} \frac{\partial \mathcal{L}}{\partial \omega_{j}} \frac{\partial \omega_{j}}{\partial \dot{q}_{i}}
\end{aligned}
$$
Substitute $q_{3}$ by $\psi$ in (2), RHS:
$$
\begin{aligned}
\frac{\partial \mathcal{L}}{\partial \psi} & =\sum_{i=1}^{3} \frac{\partial \mathcal{L}}{\partial \omega_{i}} \frac{\partial \omega_{i}}{\partial \psi} \\
& =\sum_{i=1}^{3} I_{i} \omega_{i} \frac{\partial \omega_{i}}{\partial \psi} \\
& =I_{1} \omega_{1}(\dot{\varphi} \sin \theta \cos \psi-\dot{\theta} \sin \psi)+I_{2} \omega_{2}(-\dot{\varphi} \sin \theta \sin \psi-\dot{\theta} \cos \psi)+0 \\
& =I_{1} \omega_{1} \omega_{2}+I_{2} \omega_{2}\left(-\omega_{1}\right) \\
& =\left(I_{1}-I_{2}\right) \omega_{1} \omega_{2}
\end{aligned}
$$
*this note is rearranged based on Qianye YU’s work LHS:
$$
\frac{d}{d t}\left(\frac{\partial \mathcal{L}}{\partial \dot{\psi}}\right)=I_{3} \dot{\omega}_{3}
$$
Combing (2)(4)(5) gives the first Euler dynamic equation:
$$
\left(I_{1}-I_{2}\right) \omega_{1} \omega_{2}-I_{3} \dot{\omega}_{3}=0
$$
Similarly substitute $q_{2}$ by $\varphi$ into equation(2). Since $\frac{\partial \mathcal{L}}{\partial \varphi}=0$, we have:
$$
\frac{d}{d t}\left(\frac{\partial \mathcal{L}}{\partial \dot{\varphi}}\right)=0
$$
Apply chain rule to LHS of (7) gives:
$$
\begin{aligned}
0= & I_{1} \dot{\omega}_{1} \sin \theta \sin \psi+I_{2} \dot{\omega}_{2} \sin \theta \cos \psi+I_{3} \dot{\omega}_{3} \cos \theta+I_{1} \omega_{1}(\cos \theta \sin \psi \dot{\theta} \\
& +\sin \theta \cos \psi \dot{\psi})+I_{2} \omega_{2}(\cos \theta \cos \psi \dot{\theta}-\sin \theta \sin \psi \dot{\psi})-I_{3} \omega_{3} \sin \theta \dot{\theta}
\end{aligned}
$$
We introduce $A=I_{1} \omega_{1}(\cos \theta \sin \psi \dot{\theta}+\sin \theta \cos \psi \dot{\psi})$ and $B=I_{2} \omega_{2}(\cos \theta \cos \psi \dot{\theta}-$ $\sin \theta \sin \psi \dot{\psi})$ to reduce the calculation.
Notice $I_{3} \dot{\omega}_{3}=\left(I_{1}-I_{2}\right) \omega_{1} \omega_{2}$. So (8) is equivalent to:
$$
\begin{aligned}
\sin \theta\left[I_{1} \dot{\omega}_{1} \sin \psi+I_{2} \dot{\omega}_{2} \cos \psi\right] & =\left(I_{2}-I_{1}\right) \omega_{1} \omega_{2} \cos \theta+I_{3} \omega_{3} \sin \theta \dot{\theta}-A-B \\
& =I_{1}\left(-\omega_{1} \omega_{2} \cos \theta-\omega_{1} \cos \theta \sin \psi \dot{\theta}-\omega_{1} \sin \theta \cos \psi \dot{\psi}\right) \\
& +I_{2}\left(\omega_{1} \omega_{2} \cos \theta-\omega_{2} \cos \theta \cos \psi \dot{\theta}+\omega_{2} \sin \theta \sin \psi \dot{\psi}\right) \\
& +I_{3} \omega_{3} \sin \theta \dot{\theta} \\
& =I_{1} \omega_{1}(-\dot{\varphi} \sin \theta \cos \psi \cos \theta+\dot{\theta} \sin \psi \cos \theta-\dot{\theta} \sin \psi \cos \theta\\&-\sin \theta \cos \psi \dot{\psi}) +I_{2} \omega_{2}(\dot{\varphi} \sin \theta \sin \psi \cos \theta+\dot{\theta} \cos \psi \cos \theta\\&-\dot{\theta} \cos \psi \cos \theta+\sin \theta \sin \psi \dot{\psi}) +I_{3} \omega_{3} \sin \theta \dot{\theta} \\
& =I_{1} \omega_{1}(-\dot{\varphi} \sin \theta \cos \psi \cos \theta-\sin \theta \cos \psi \dot{\psi}) \\
& +I_{2} \omega_{2}(\dot{\varphi} \sin \theta \sin \psi \cos \theta+\sin \theta \sin \psi \dot{\psi}) \\
& +I_{3} \omega_{3} \sin \theta \dot{\theta}
\end{aligned}
$$
Dividing (9) through $\sin \theta$ gives:
$$
\begin{aligned}
I_{1} \dot{\omega}_{1} \sin \psi+I_{2} \dot{\omega}_{2} \cos \psi & =I_{1} \omega_{1}(-\dot{\varphi} \cos \psi \cos \theta-\cos \psi \dot{\psi}) \\
& +I_{2} \omega_{2}(\dot{\varphi} \sin \psi \cos \theta+\sin \psi \dot{\psi}) \\
& +I_{3} \omega_{3} \dot{\theta}
\end{aligned}
$$
We keep equation (10) for later use
Substituting $q_{3}$ by $\theta$ into equation $(2)$ :
$$
\frac{d}{d t}\left(\frac{\partial \mathcal{L}}{\partial \dot{\theta}}\right)=\frac{\partial \mathcal{L}}{\partial \theta}
$$
So,
$$
\begin{aligned}
\frac{d}{d t}\left(I_{1} \omega_{1} \cos \psi-I_{2} \omega_{2} \sin \psi\right)= & I_{1} \omega_{1} \dot{\varphi} \cos \theta \sin \psi+I_{2} \omega_{2} \dot{\varphi} \cos \theta \cos \psi \\
& +I_{3} \omega_{3} \dot{\varphi}(-\sin \theta)
\end{aligned}
$$
which gives:
$$
\begin{aligned}
I_{1} \dot{\omega}_{1} \cos \psi-I_{2} \dot{\omega}_{2} \sin \psi= & I_{1} \omega_{1}(\dot{\varphi} \cos \theta \sin \psi+\sin \psi \dot{\psi}) \\
& +I_{2} \omega_{2}(\dot{\varphi} \cos \theta \cos \psi+\cos \psi \dot{\psi}) \\
& -I_{3} \omega_{3} \dot{\varphi} \sin \theta
\end{aligned}
$$
Since (10) and (13) are obtained from EL equation of generalized coordinates $\varphi$ and $\theta$ respectively, along with (6), we have used all three independent EL equations, the other two Euler equations must be obtained directly from combinations of (10) and (13):
Firstly, (10) $\cdot \sin \psi+(13) \cdot \cos \psi$ gives:
$$
\begin{aligned}
I_{1} \dot{\omega}_{1} & =I_{2} \omega_{2}(\dot{\varphi} \cos \theta+\dot{\psi})+I_{3} \omega_{3}(\dot{\theta} \sin \psi-\dot{\varphi} \sin \theta \cos \psi) \\
& =I_{2} \omega_{2} \omega_{3}+I_{3} \omega_{3}\left(-\omega_{2}\right) \\
& =\left(I_{2}-I_{3}\right) \omega_{2} \omega_{3}
\end{aligned}
$$
And $(10) \cdot \cos \psi-(13) \cdot \sin \psi$ gives:
$$
\begin{aligned}
I_{2} \dot{\omega}_{2} & =I_{1} \omega_{1}(-\dot{\varphi} \cos \theta-\dot{\psi})+I_{3} \omega_{3}(\dot{\theta} \cos \psi+\dot{\varphi} \sin \theta \sin \psi) \\
& =I_{1} \omega_{1}\left(-\omega_{3}\right)+I_{3} \omega_{3} \omega_{1} \\
& =\left(I_{3}-I_{1}\right) \omega_{3} \omega_{1}
\end{aligned}
$$
Rearranging (6),(14),(15) gives the Eulerian dynamic equations:
$$
\left\{\begin{array}{l}
\left(I_{1}-I_{2}\right) \omega_{1} \omega_{2}-I_{3} \dot{\omega}_{3}=0 \\
\left(I_{2}-I_{3}\right) \omega_{2} \omega_{3}-I_{1} \dot{\omega}_{1}=0 \\
\left(I_{3}-I_{1}\right) \omega_{3} \omega_{1}-I_{2} \dot{\omega}_{2}=0
\end{array}\right.
$$