MIT8.04 [part7]
Expectation values of ˆx. Wave-packets and uncertainty. Time evolution of wave-packets. Shape changes. Fourier transforms and Parseval Theorem.
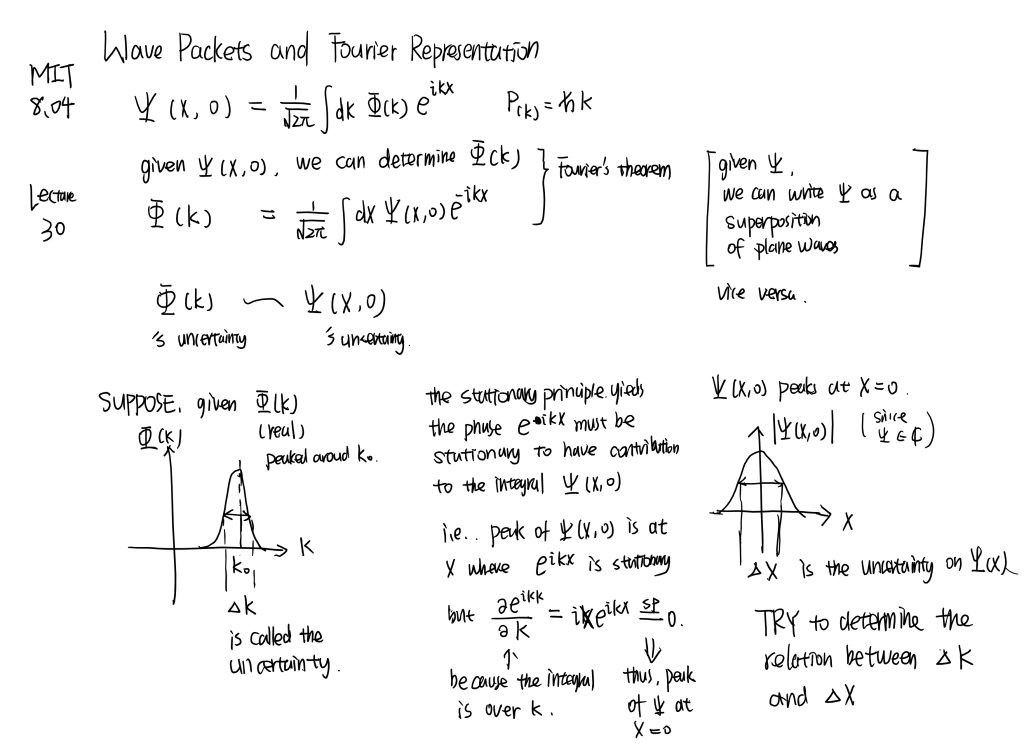
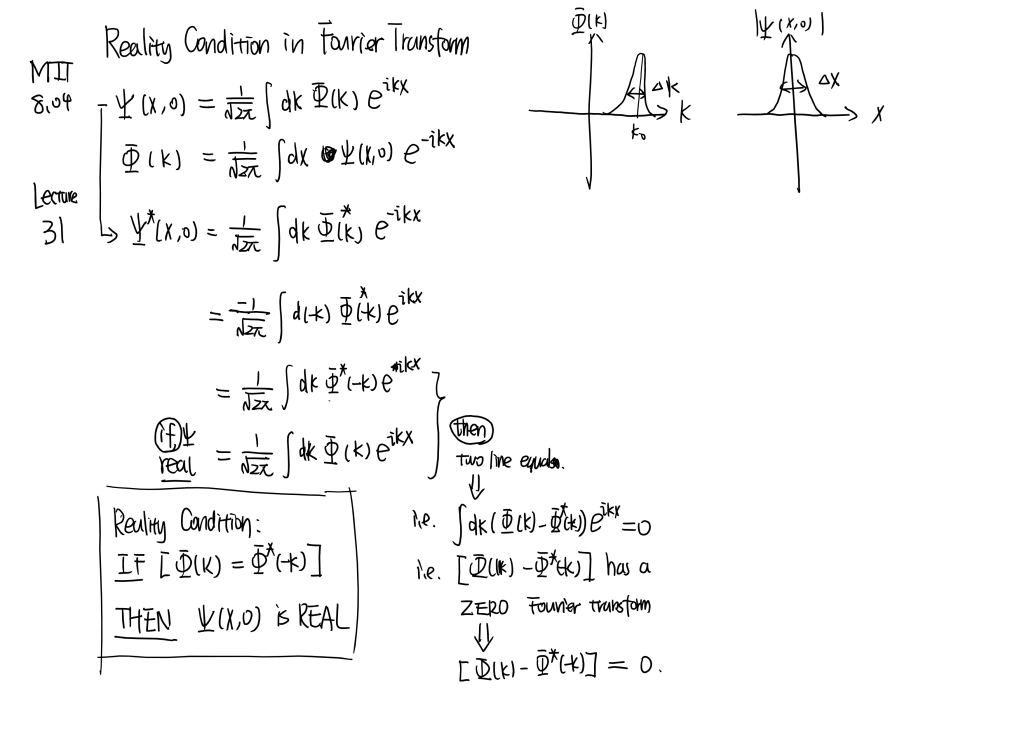

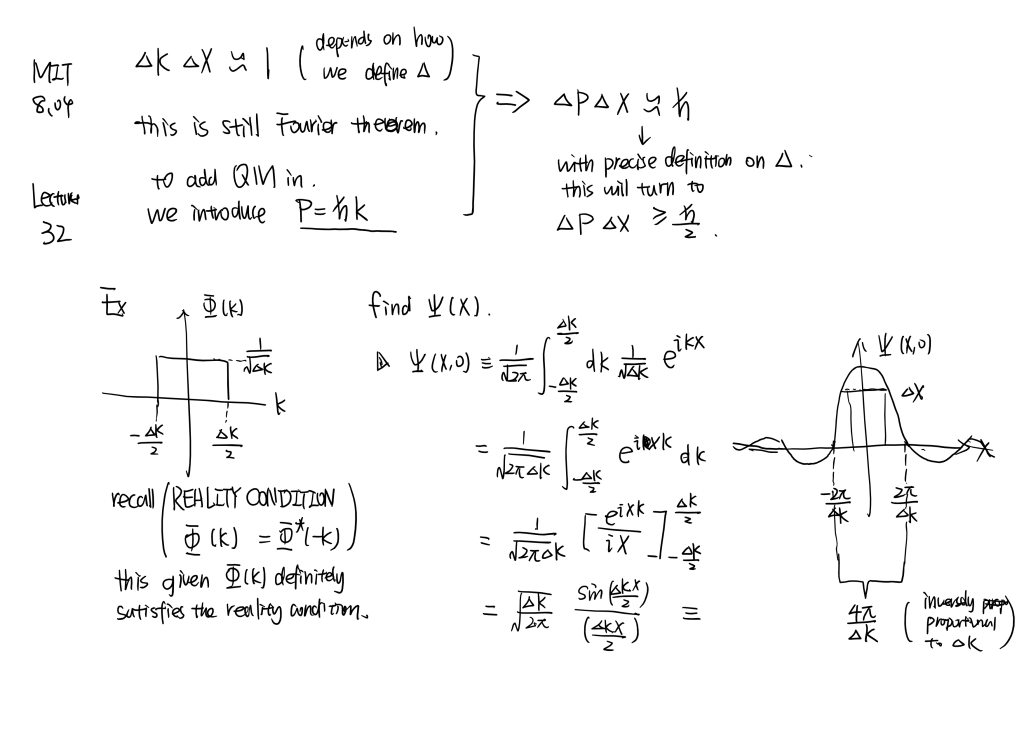
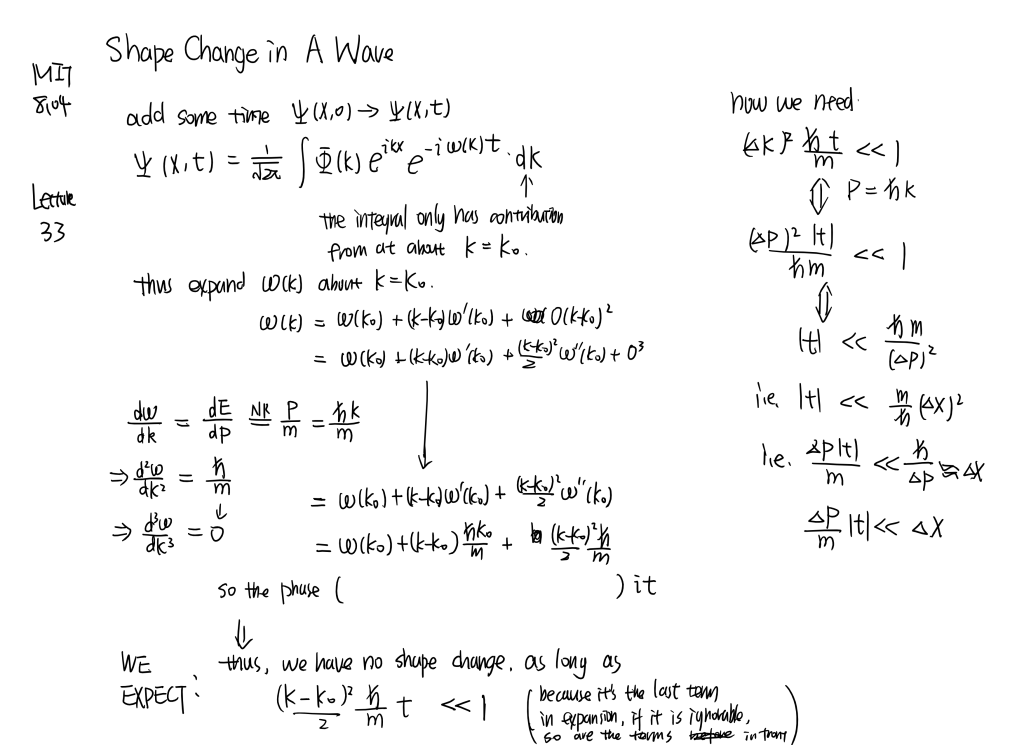







MIT8.04 [part7]
Expectation values of ˆx. Wave-packets and uncertainty. Time evolution of wave-packets. Shape changes. Fourier transforms and Parseval Theorem.




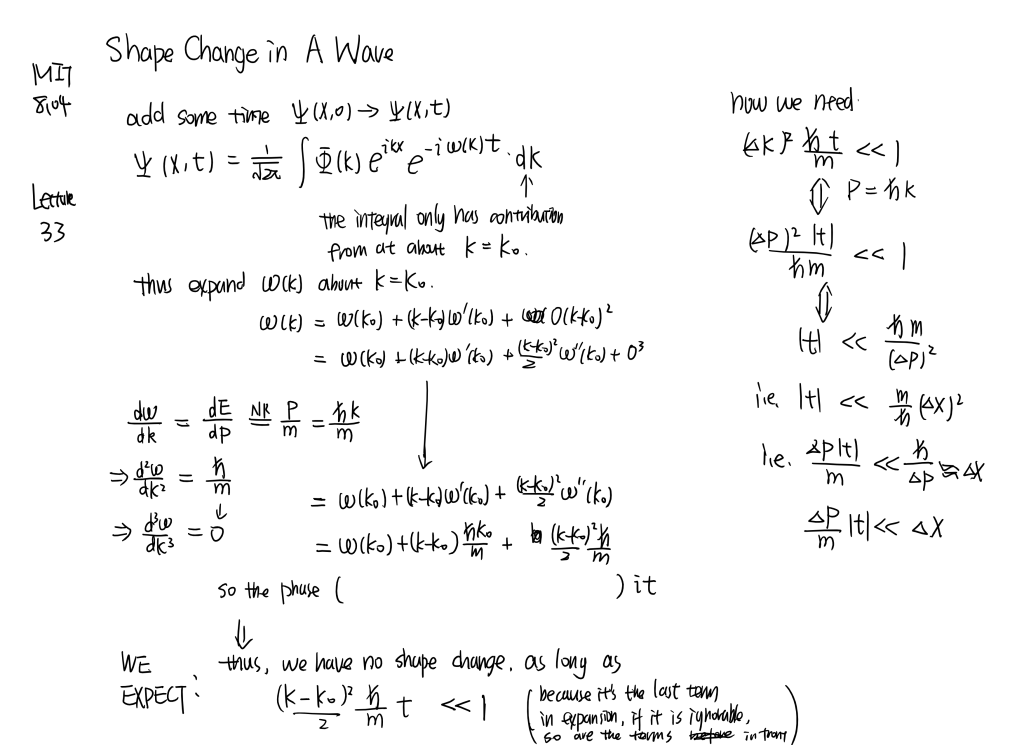







MIT8.04 [part6]
Interpretation of the wavefunction. Probability density, probability current. Current conservation. Hermitian operators.






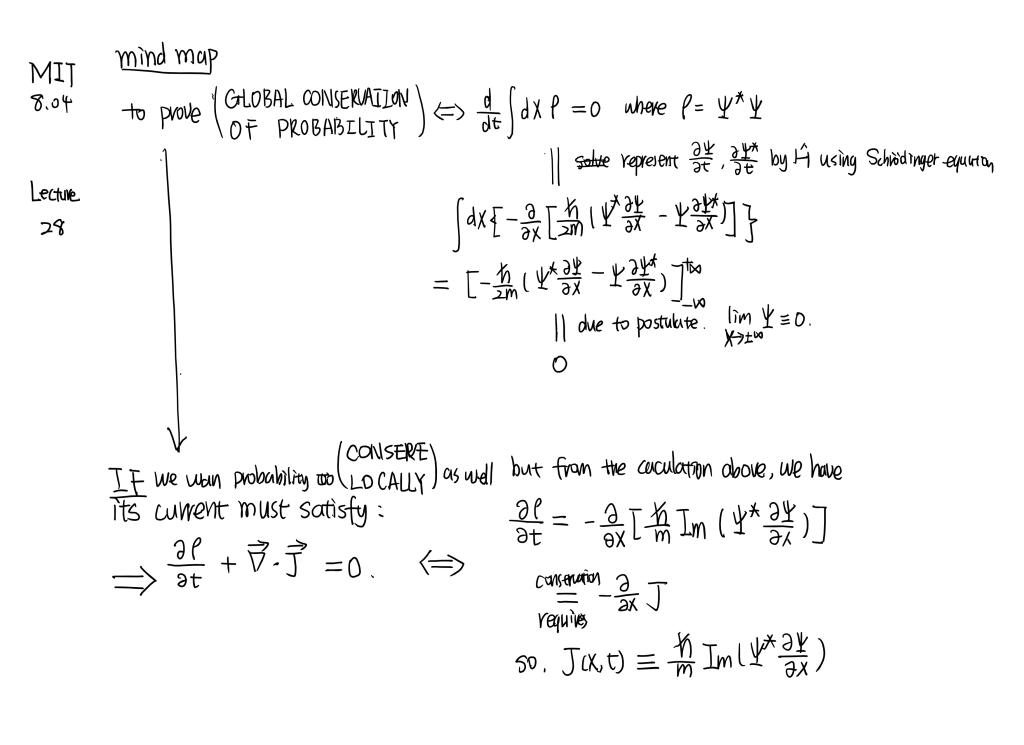

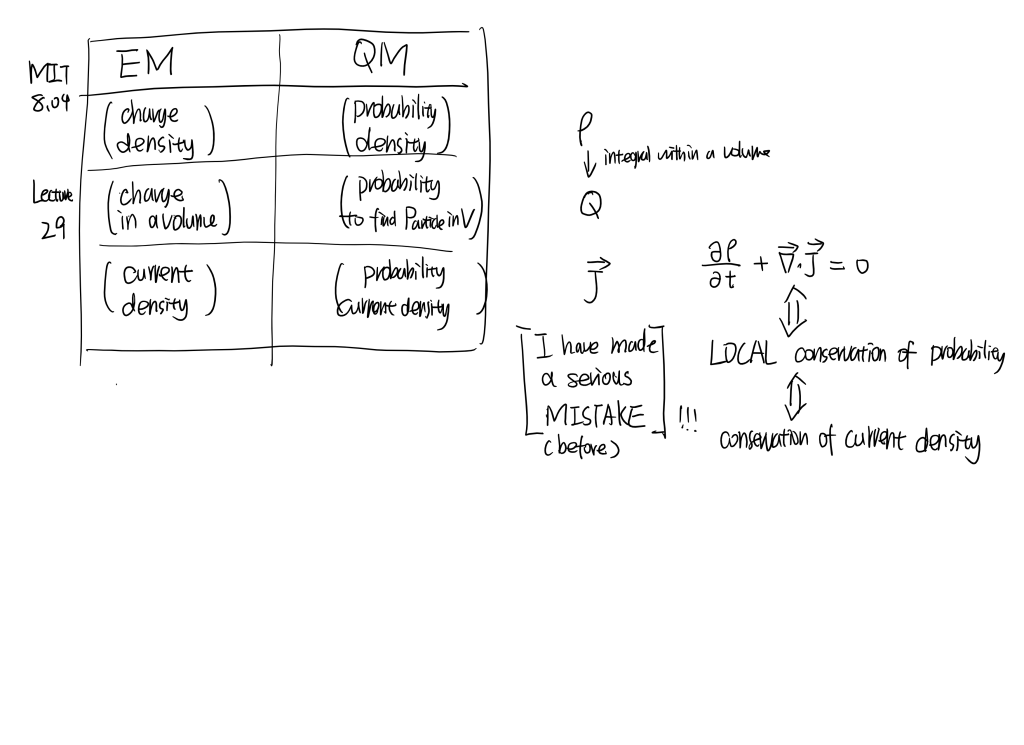
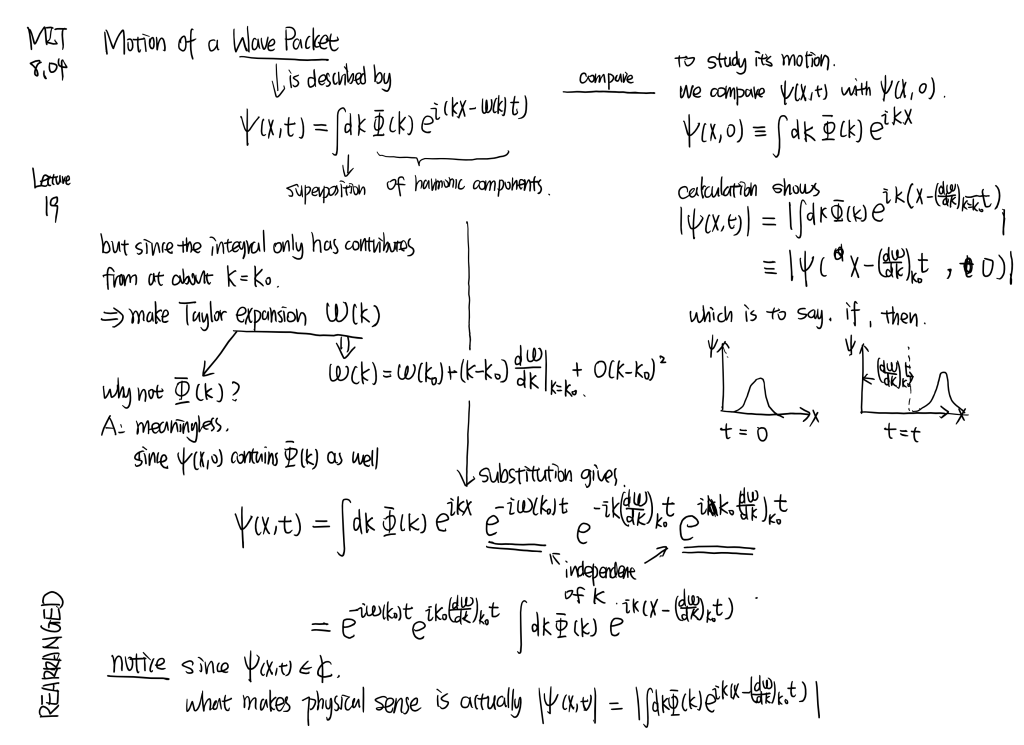
MIT8.04 [part5]
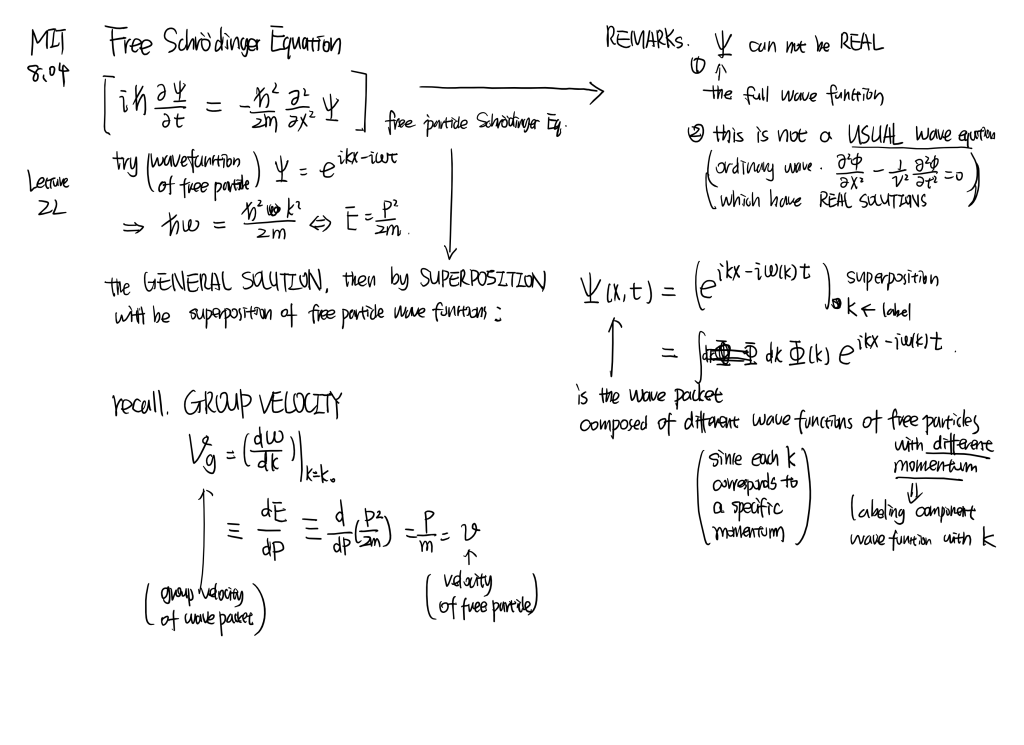
Matter wave for a particle. Momentum and position operators. Schrödinger equation.


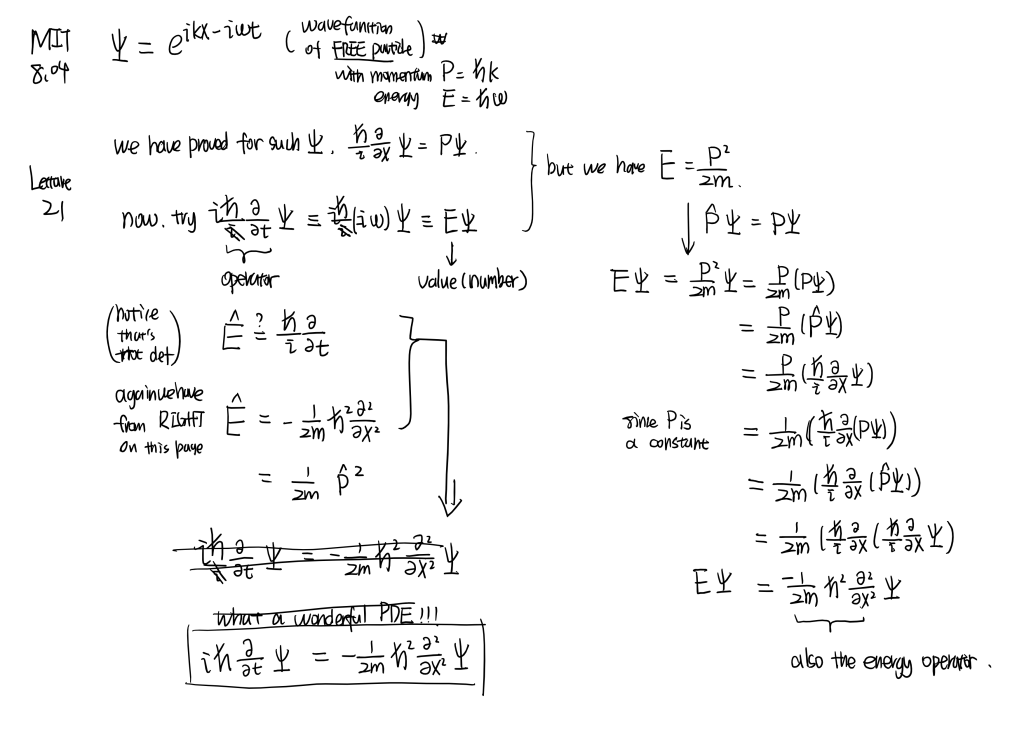



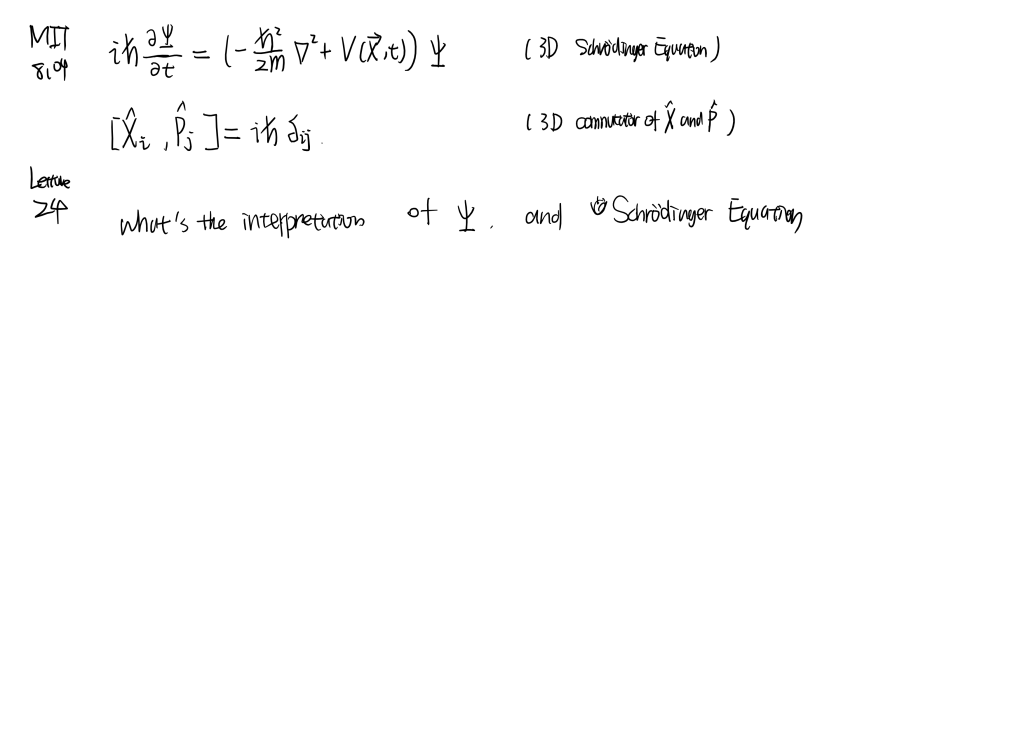
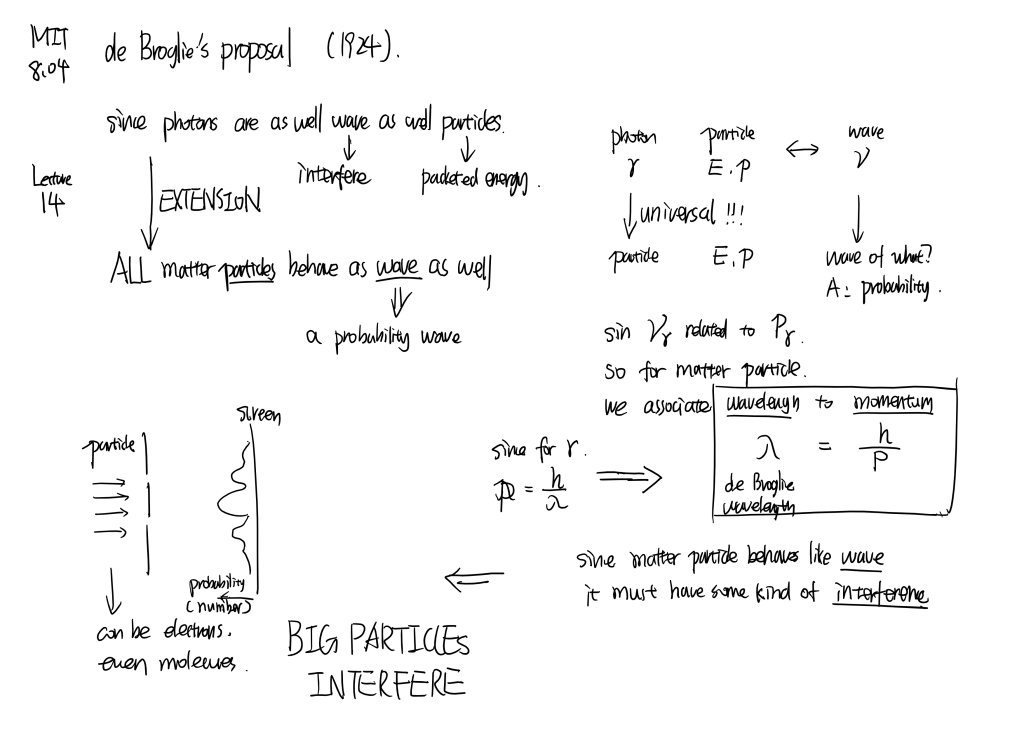
MIT8.04 [part4]
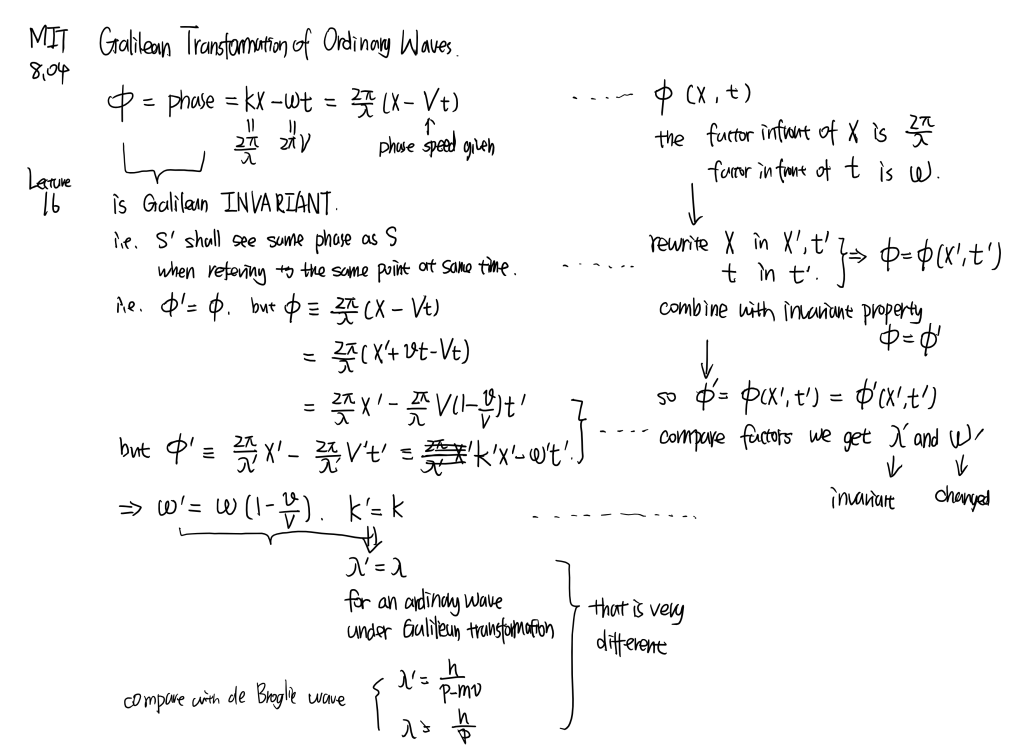
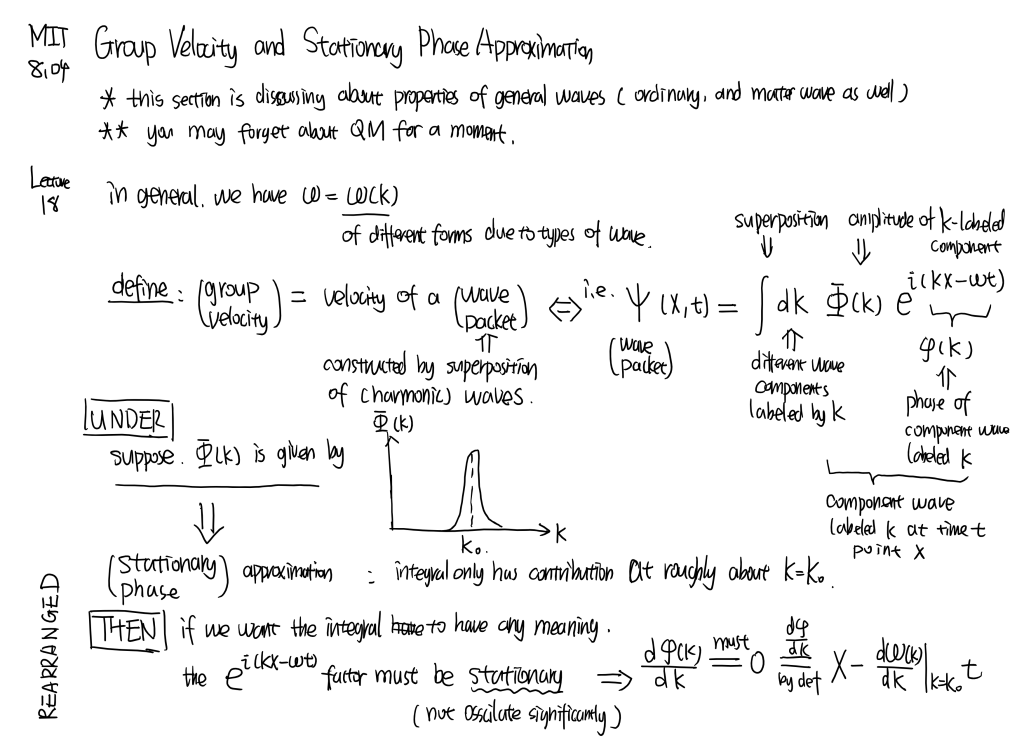
Galilean transformation of de Broglie wavelength. Wave-packets and group velocity.




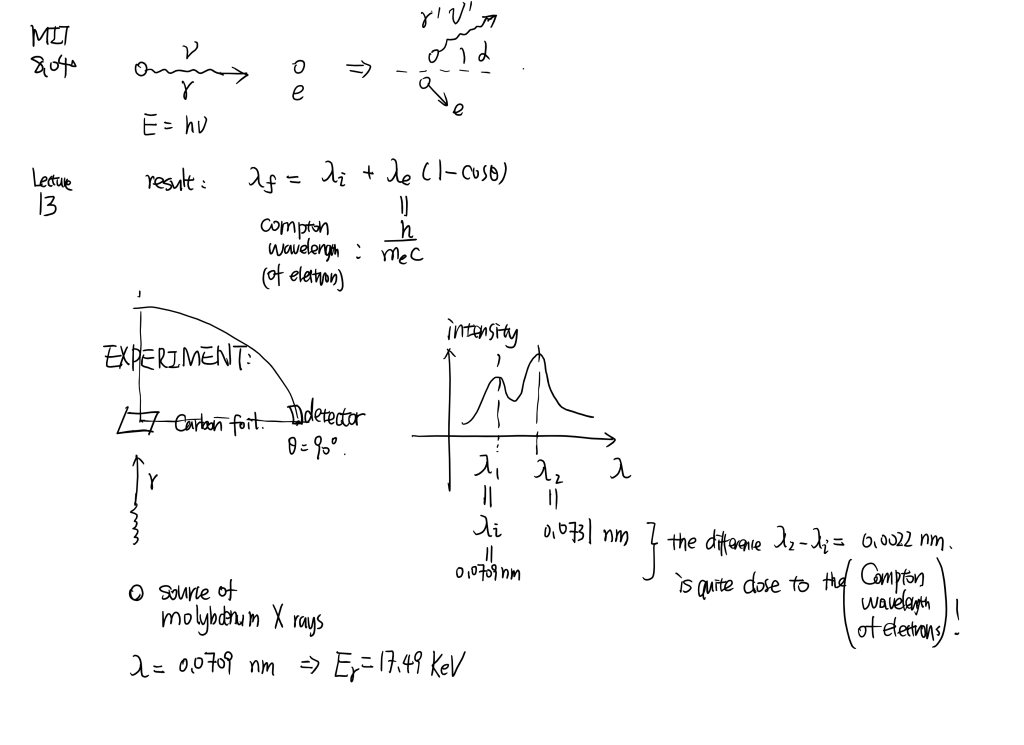
MIT8.04 [part3]
Photoelectric effect. Compton Scattering. de Broglie wavelength.




All links redirect to original MIT Open Course Ware files
Incase you encounter any problem due to regional internet policy, email the website administrator for a copy of the material.
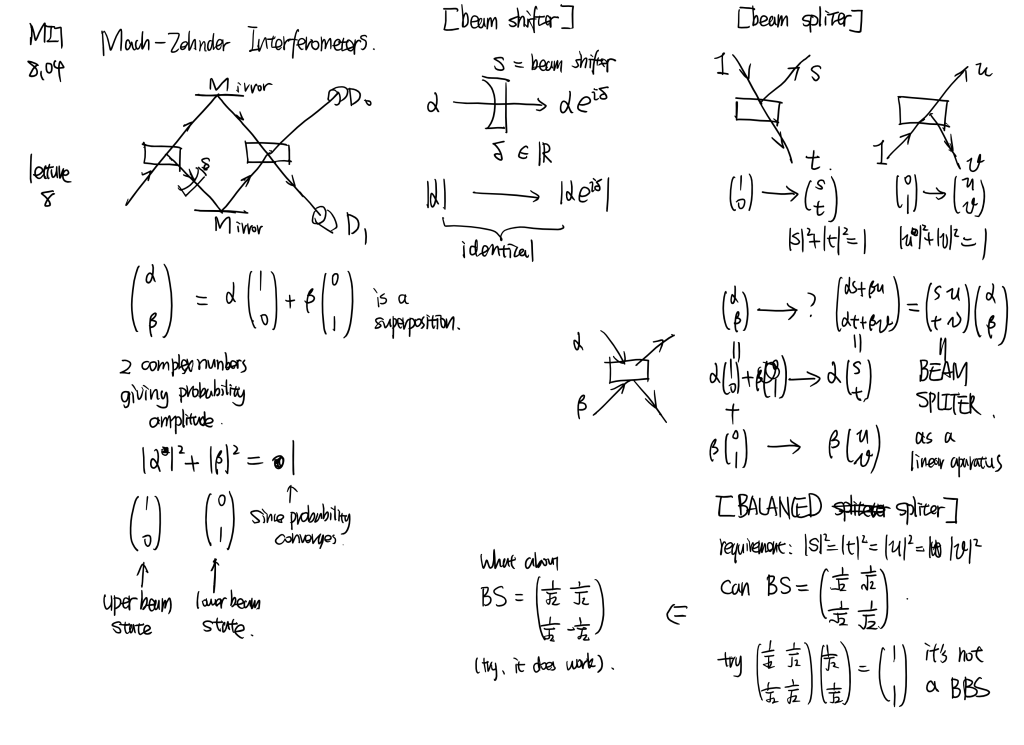
MIT8.04 [part2]
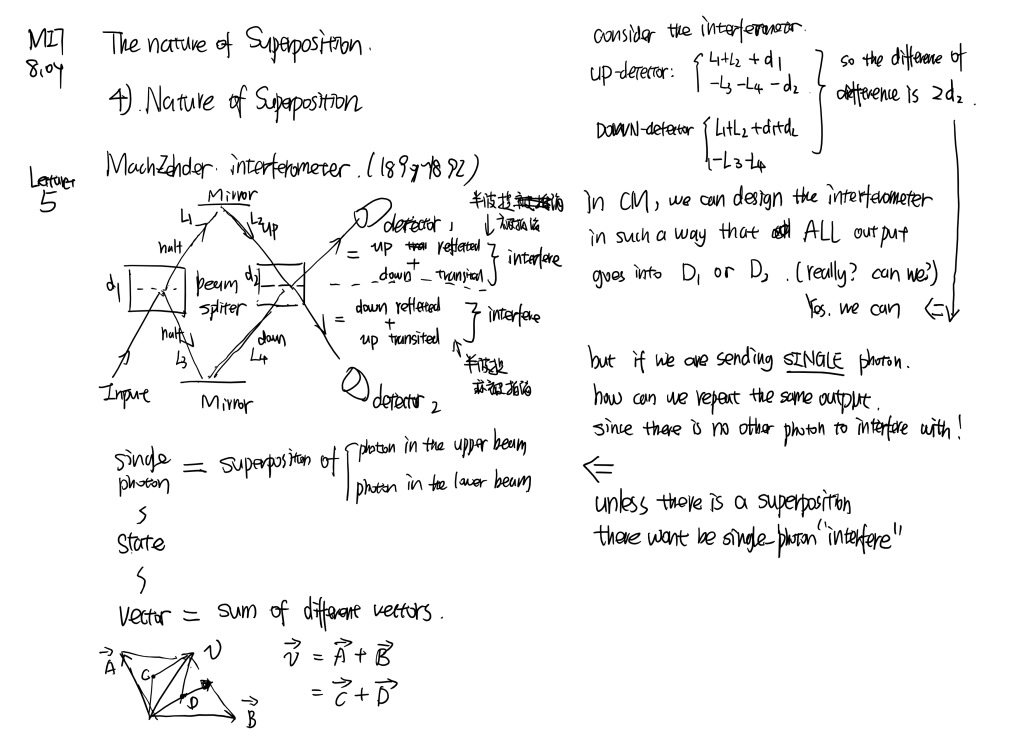
Mach-Zehnder interferometer and Elitzur-Vaidman bomb
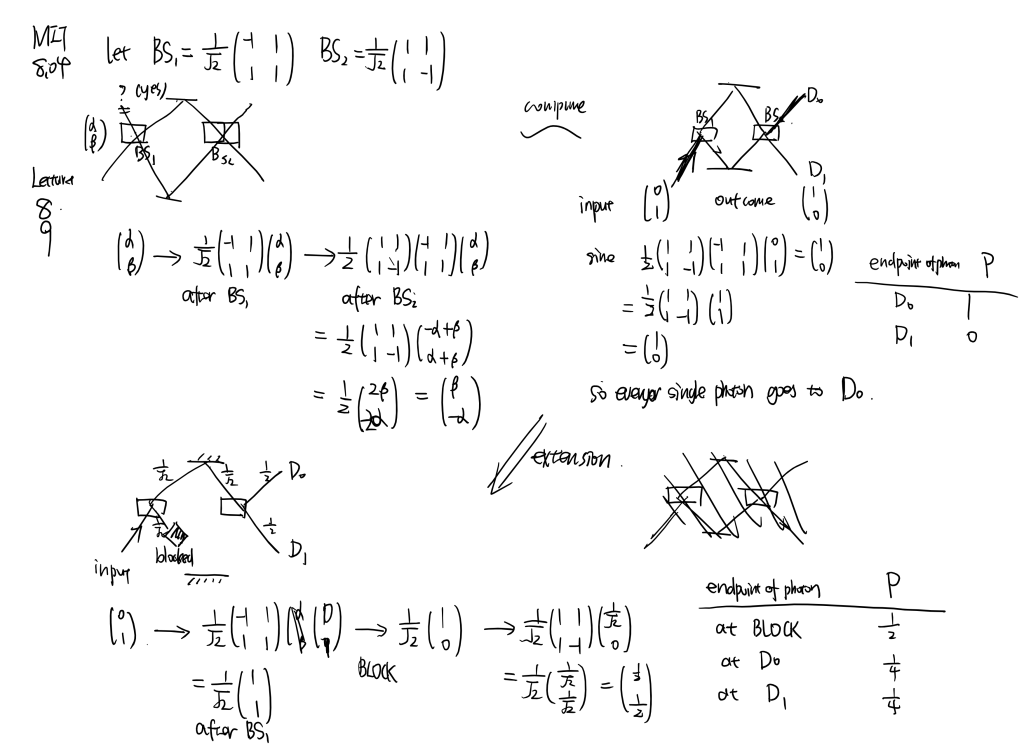
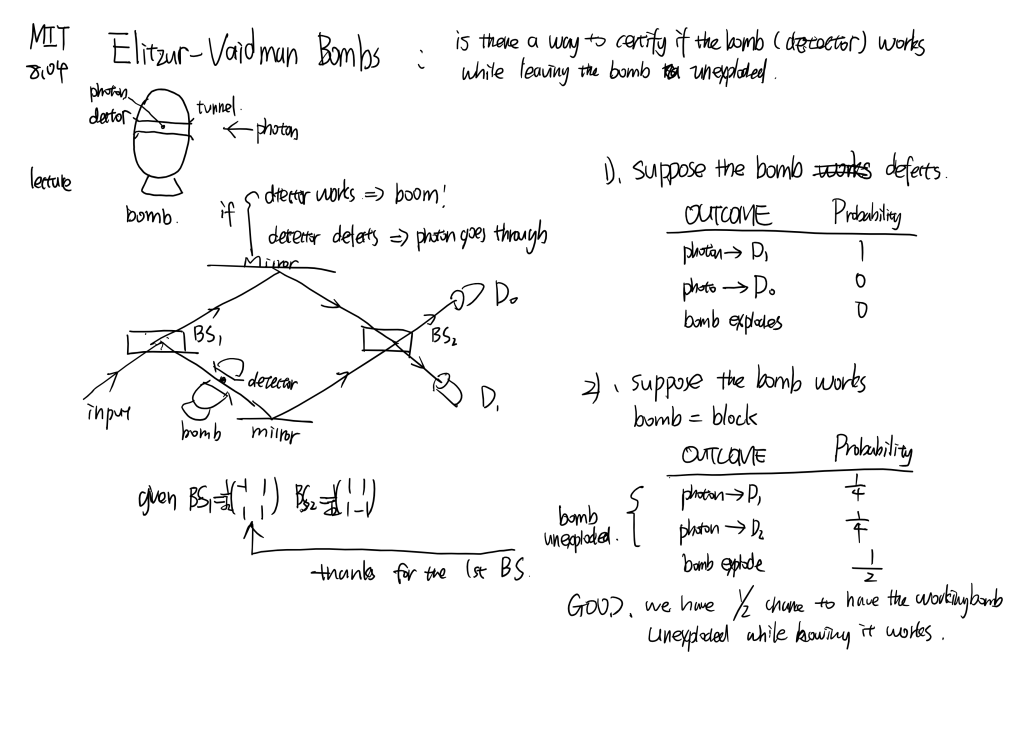
MIT8.04 [part1]
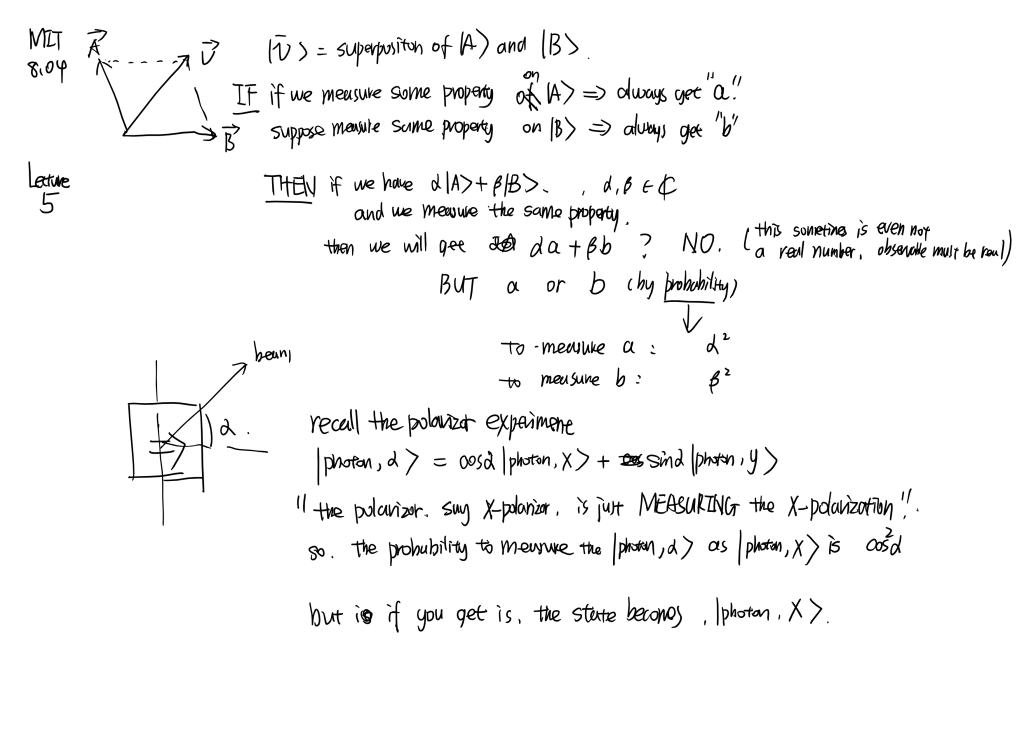
Linearity and superposition, linear operator, Schrodinger equation, necessity of complex number, Mach-Zehnder interferometer, polarizer experiment and spin experiment…
original resource at MITOpenCourseWare

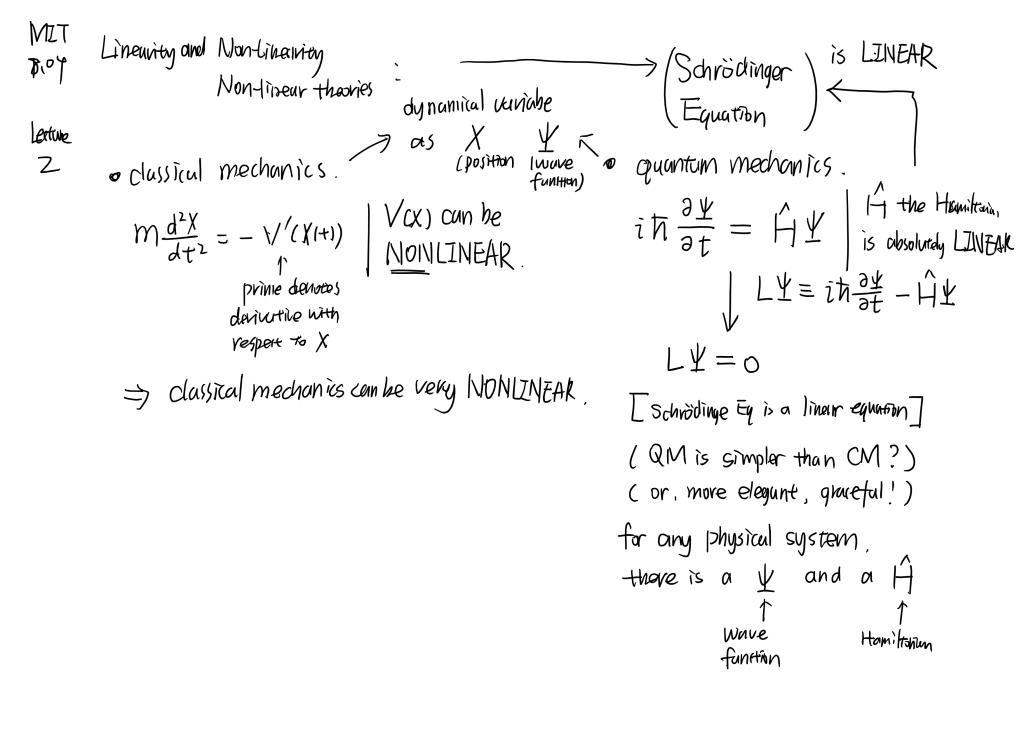

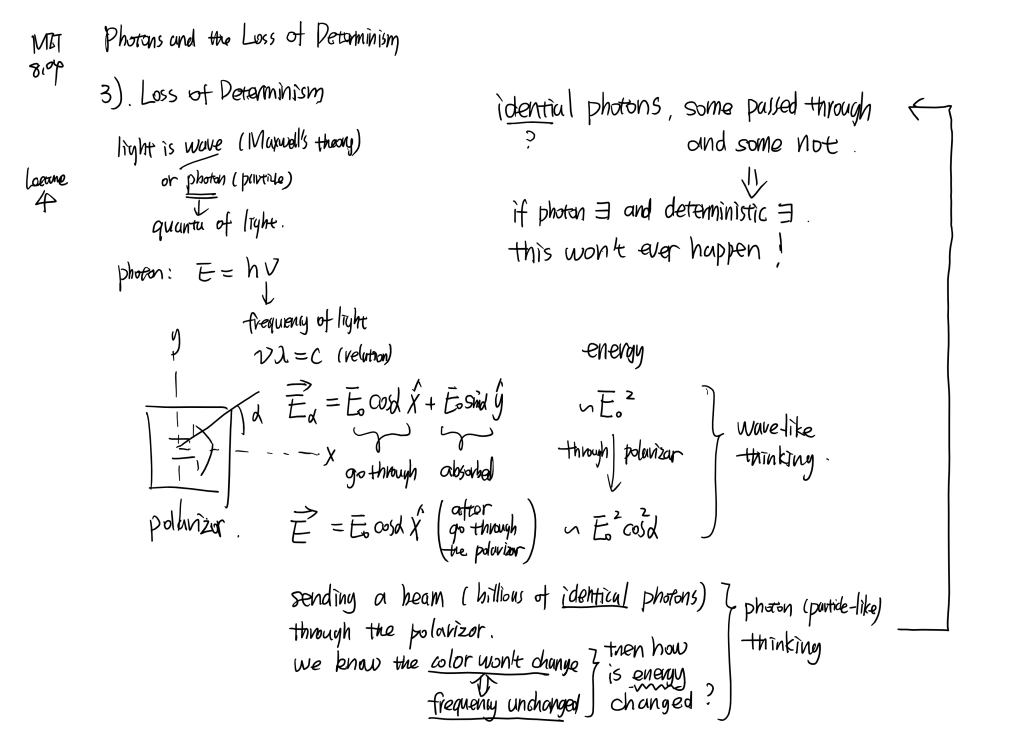



1.6 Strange Particles
Discovery of Kaon, “strangeness”, and its “conservation law”
![notes on 1.6 Strange Particles [part 1]](https://physics.run/wp-content/uploads/2023/01/WCM0058.png)
![notes on 1.6 Strange Particles [part2]](https://physics.run/wp-content/uploads/2023/01/WCM0059.png)
![notes on 1.6 Strange Particles [part 3]](https://physics.run/wp-content/uploads/2023/01/WCM0060.png)
1.5 Neutrinos
The indeterministic electron energy in beta decay raised a requirement of new particle produced in the reaction, recalling Powell’s emulsion picture indicates this new particle should be electrically neutral, eventually led to the family of leptons.
![notes on 1.5 Neutrinos [part1]](https://physics.run/wp-content/uploads/2023/01/WCM0053.png)
![notes on 1.5 Neutrinos [part2]](https://physics.run/wp-content/uploads/2023/01/WCM0054.png)
![notes on 1.5 Neutrinos [part3]](https://physics.run/wp-content/uploads/2023/01/WCM0055.png)
![notes on 1.5 Neutrinos [part4]](https://physics.run/wp-content/uploads/2023/01/WCM0056.png)
![notes on 1.5 Neutrinos [part5]](https://physics.run/wp-content/uploads/2023/01/WCM0057.png)