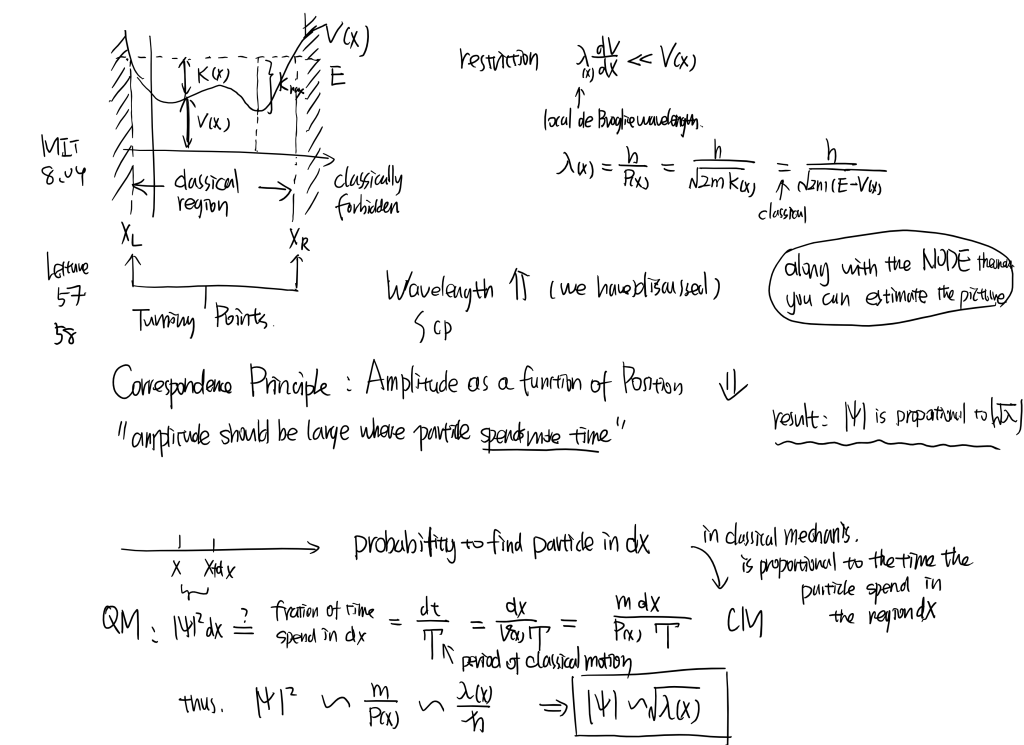
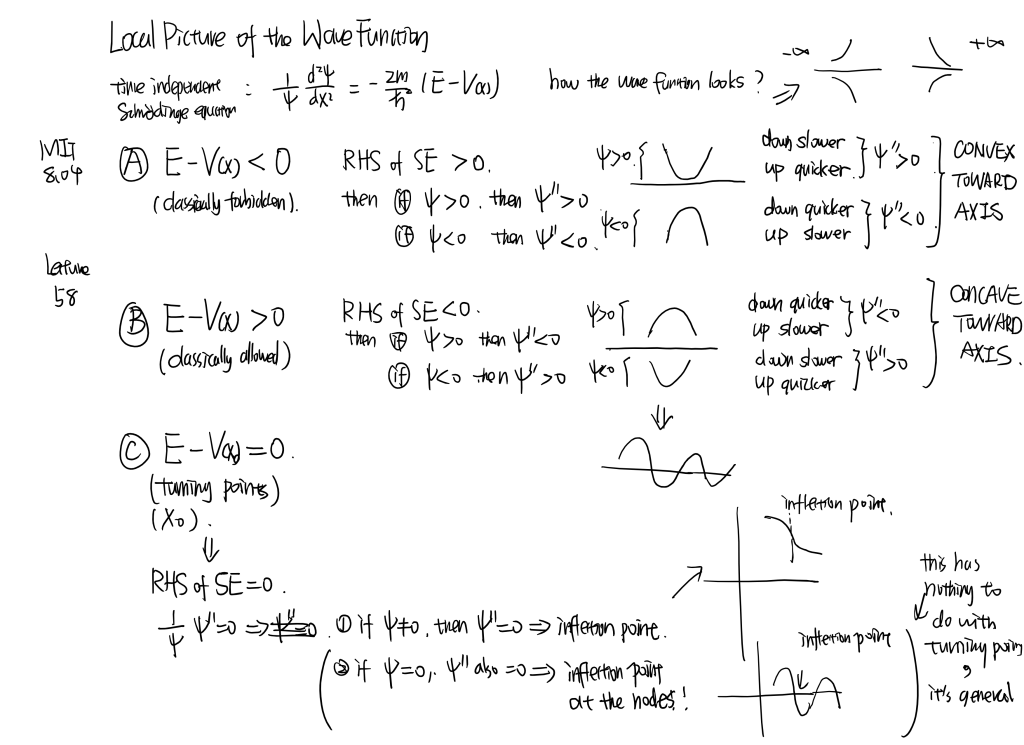
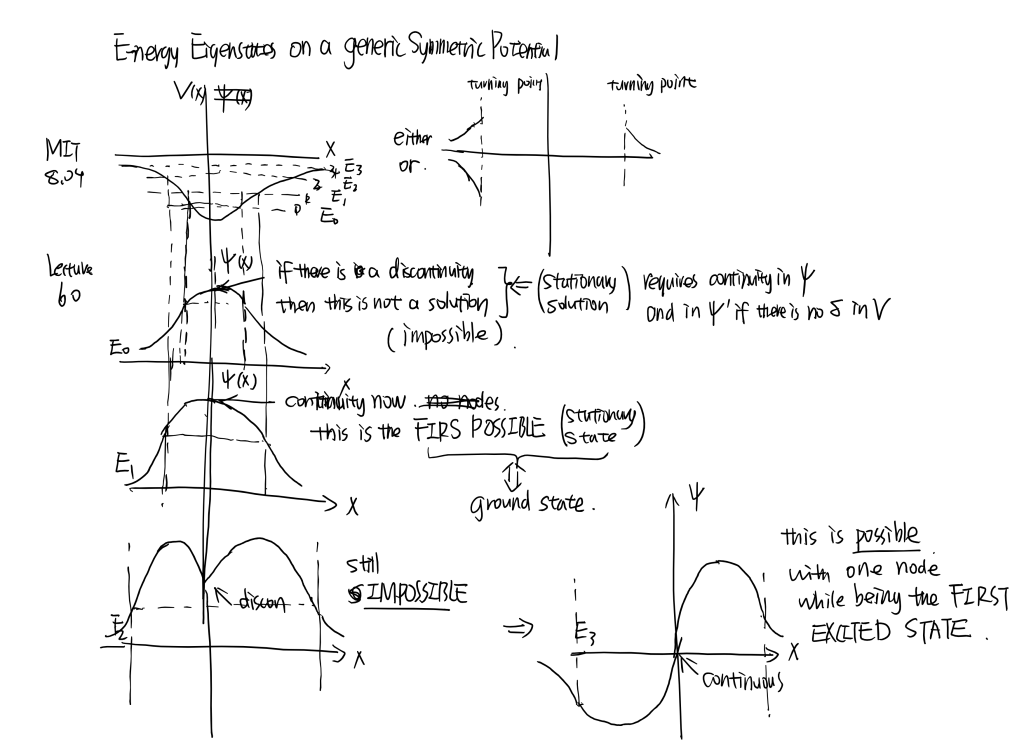
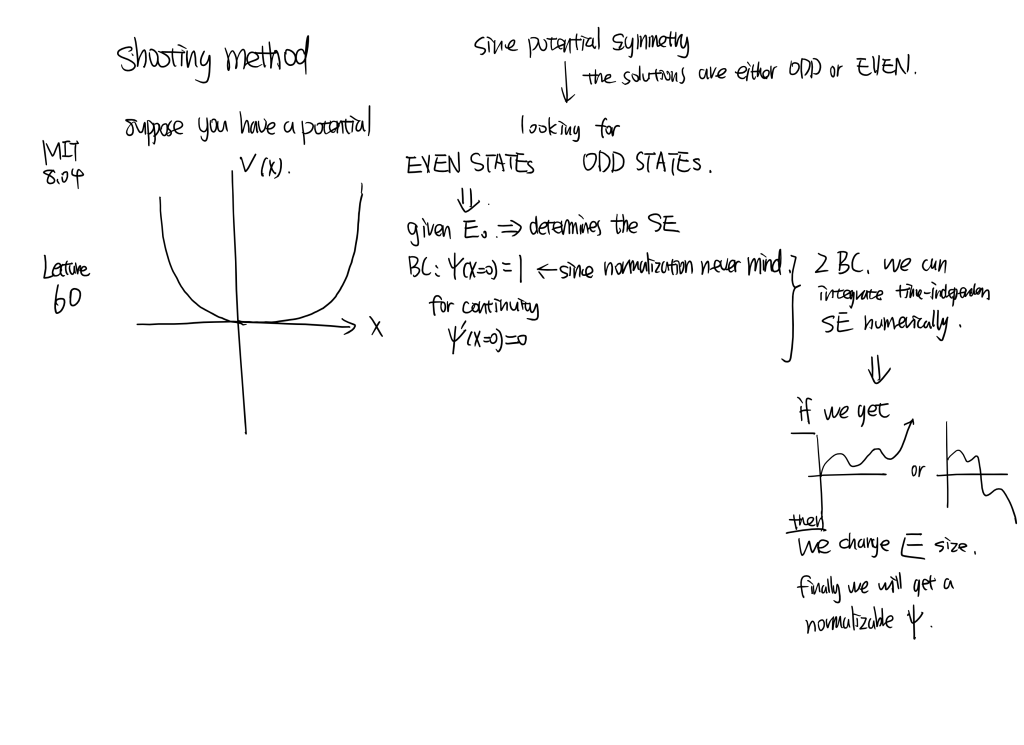
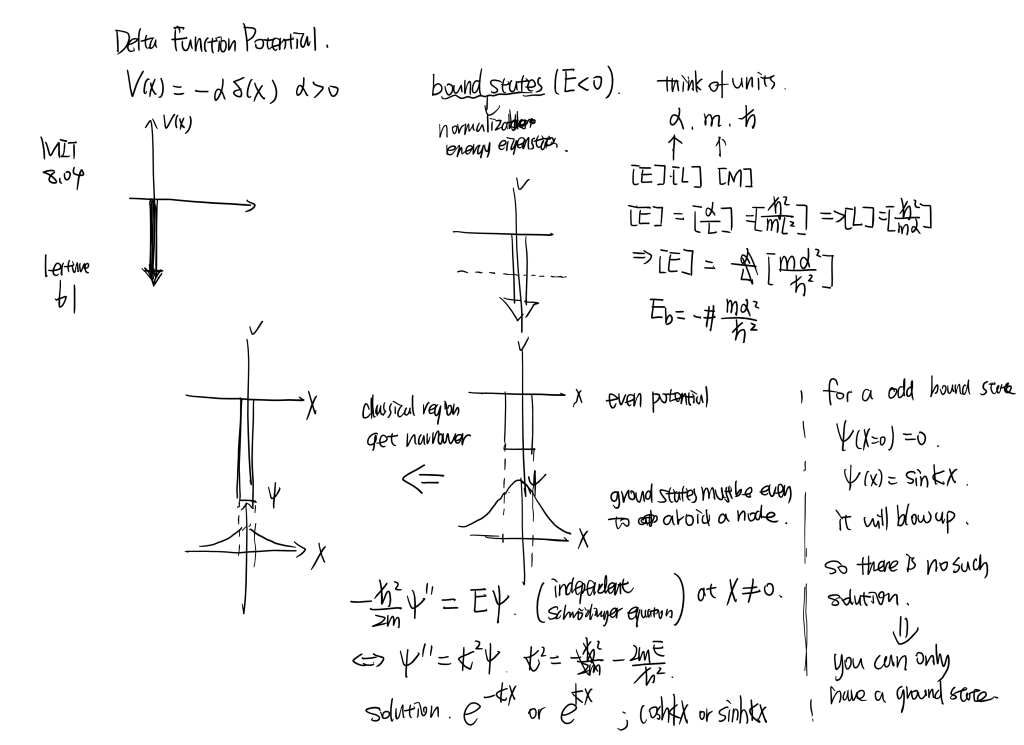
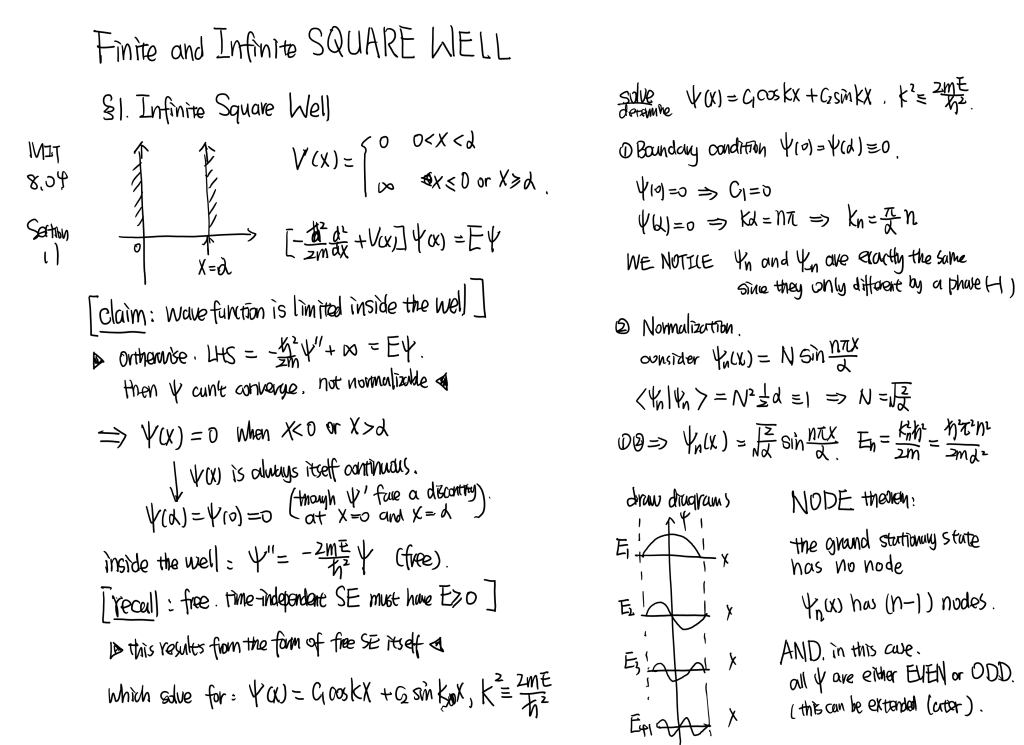
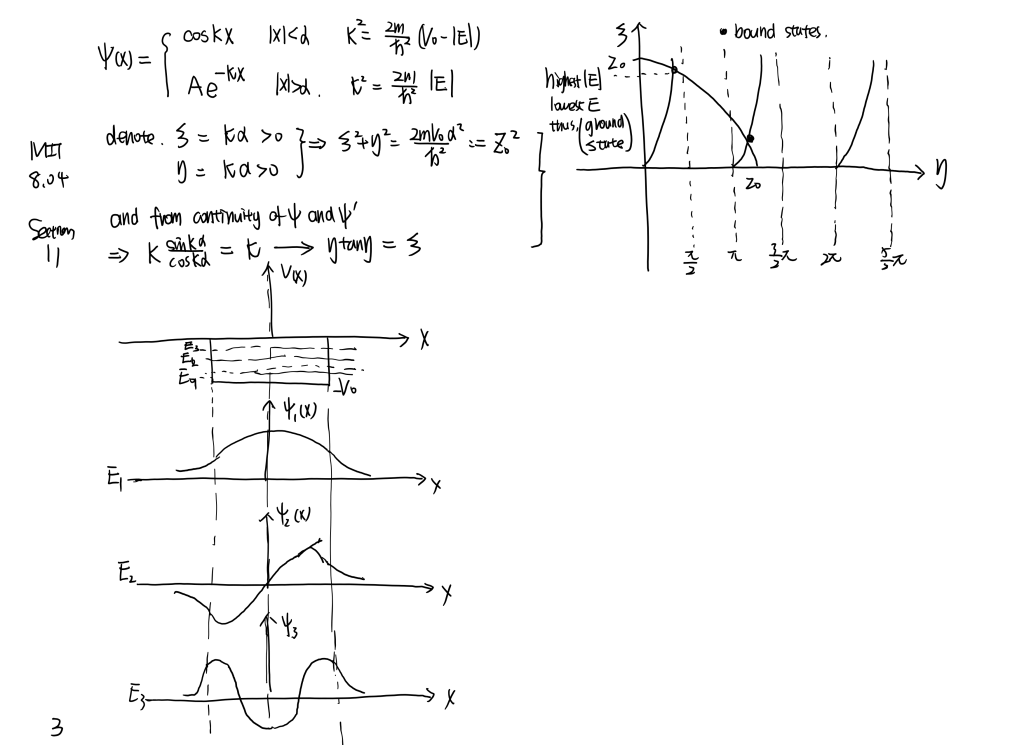
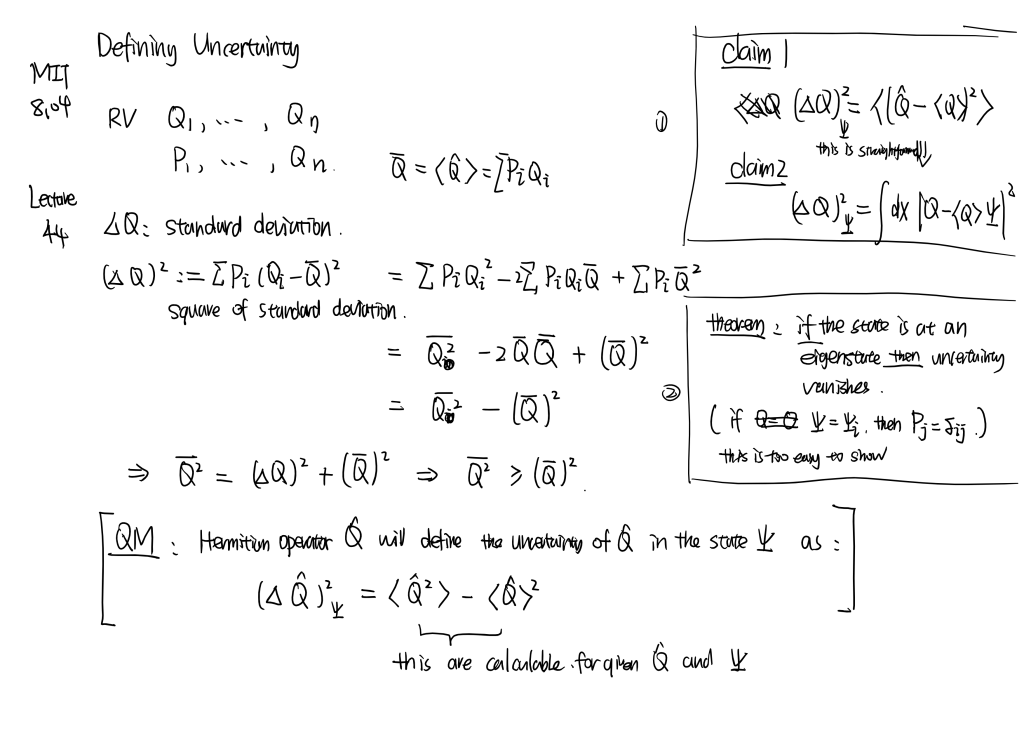
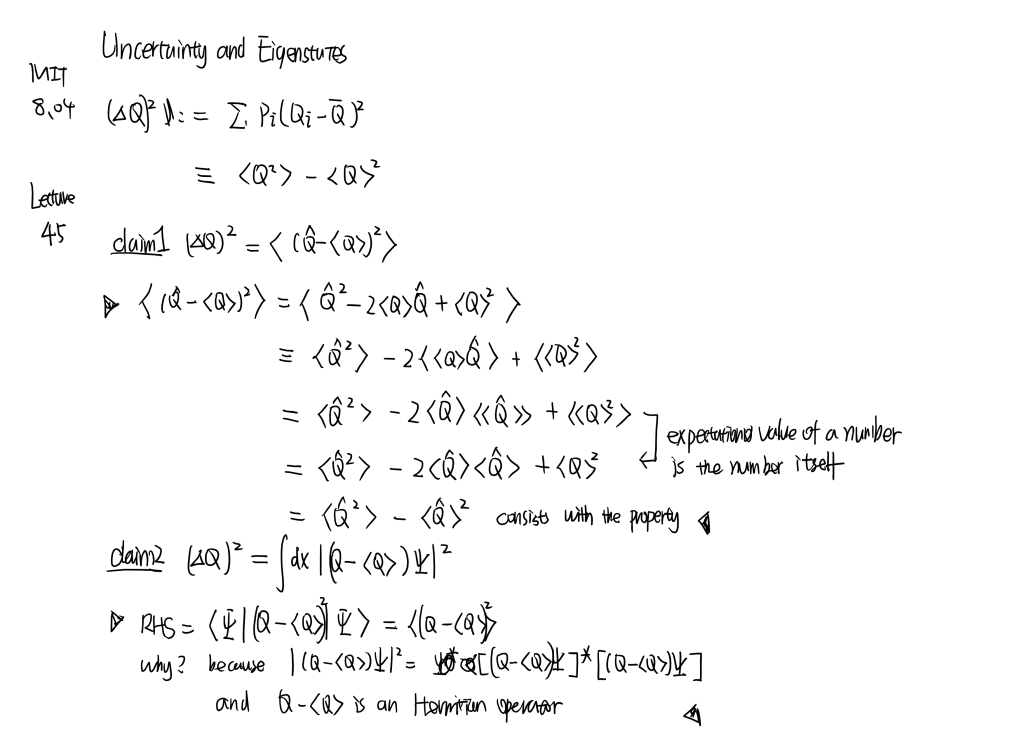MIT8.04 [part1] Linearity and superposition, linear operator, Schrodinger equation, necessity of complex number, Mach-Zehnder interferometer, polarizer experiment and spin experiment......
Read More
MIT8.04 [part2] Mach-Zehnder interferometer and Elitzur-Vaidman bomb MIT 8.04 Complete Video link Guide page other notes
Read More
MIT8.04 [part4] Galilean transformation of de Broglie wavelength. Wave-packets and group velocity. MIT 8.04 Complete Video link Guide page other...
Read More
MIT8.04 [part5] Matter wave for a particle. Momentum and position operators. Schrödinger equation. MIT 8.04 Complete Video link Guide page...
Read More
MIT8.04 [part6] Interpretation of the wavefunction. Probability density, probability current. Current conservation. Hermitian operators. MIT 8.04 Complete Video link Guide...
Read More
MIT8.04 [part7] Expectation values of ˆx. Wave-packets and uncertainty. Time evolution of wave-packets. Shape changes. Fourier transforms and Parseval Theorem....
Read More
MIT8.04 [part8] Momentum expectation values. General definition of expectation values of Hermitian operators. Time derivative of expectation values (Ehrenfest theorem)....
Read More
MIT8.04 [part9] Hermitian operators as observables: Real eigenvalues orthogonal eigenfunctions. Measurement postulate. Uncertainty defined. Uncertainty relation stated. MIT 8.04 Complete...
Read More
MIT8.04 [part10] Stationary states. Boundary conditions for the wavefunction. Particle on a circle. MIT 8.04 Complete Video link Guide page...
Read More
MIT8.04 [part11] Finite and infinite square well MIT 8.04 Complete Video link Guide page other notes
Read More
MIT8.04 [part12] The Dirac Well and Scattering off the Finite Step MIT 8.04 Complete Video link Guide page other notes
Read More
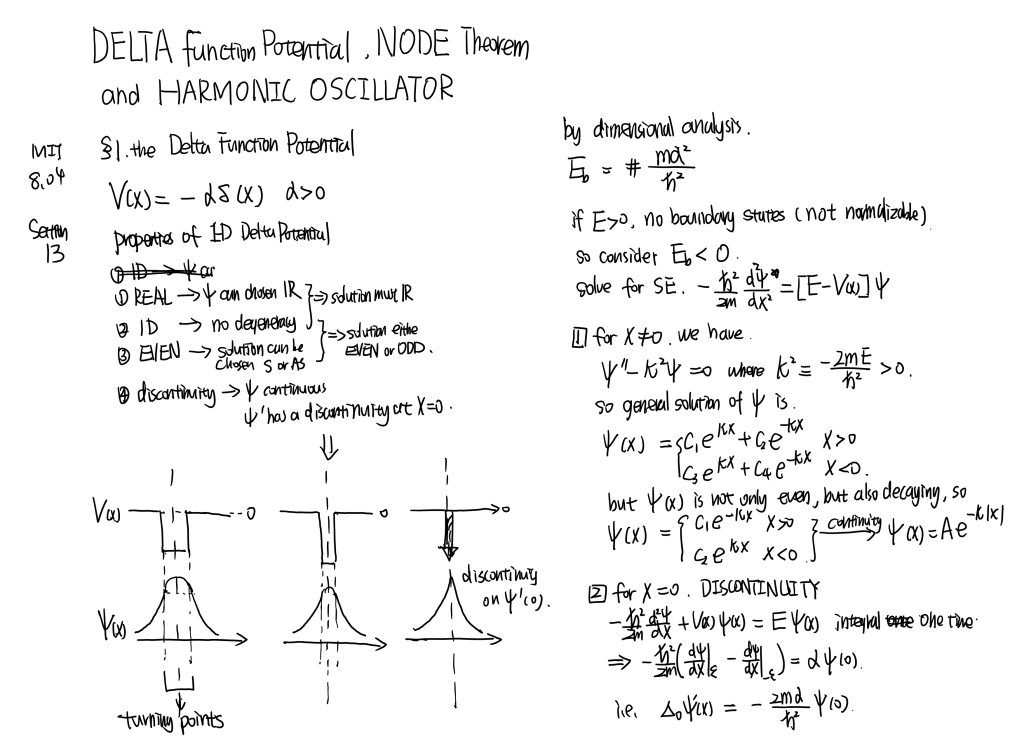
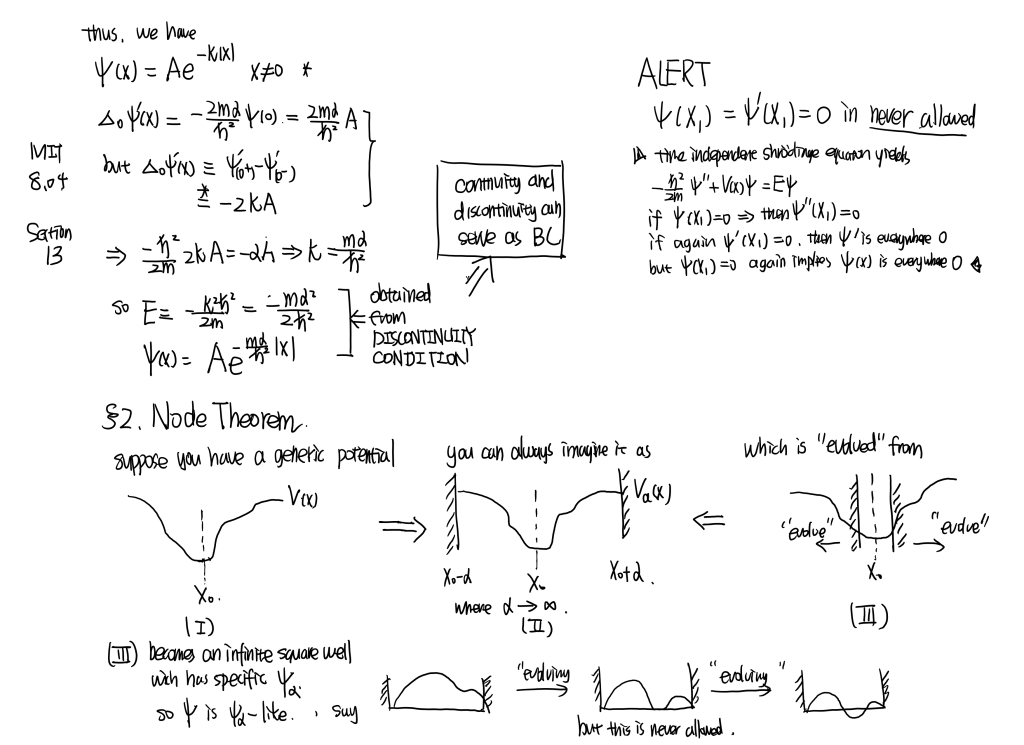
MIT8.04 [part13] Δ function potential and harmonic oscillator MIT 8.04 Complete Video link Guide page other notes
Read More
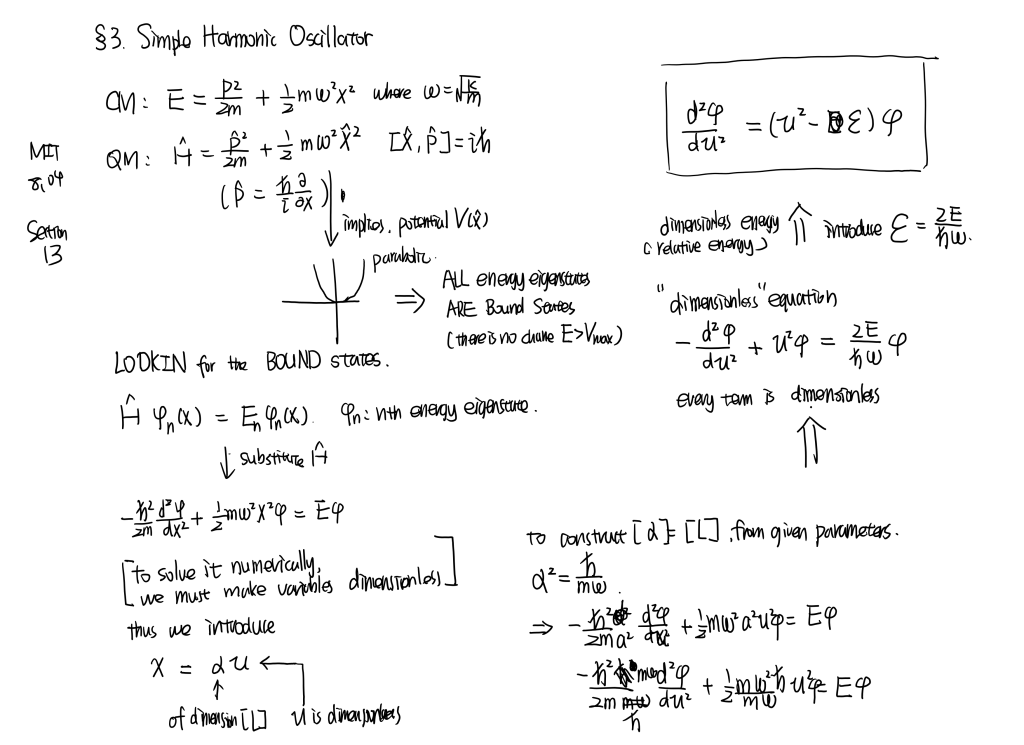
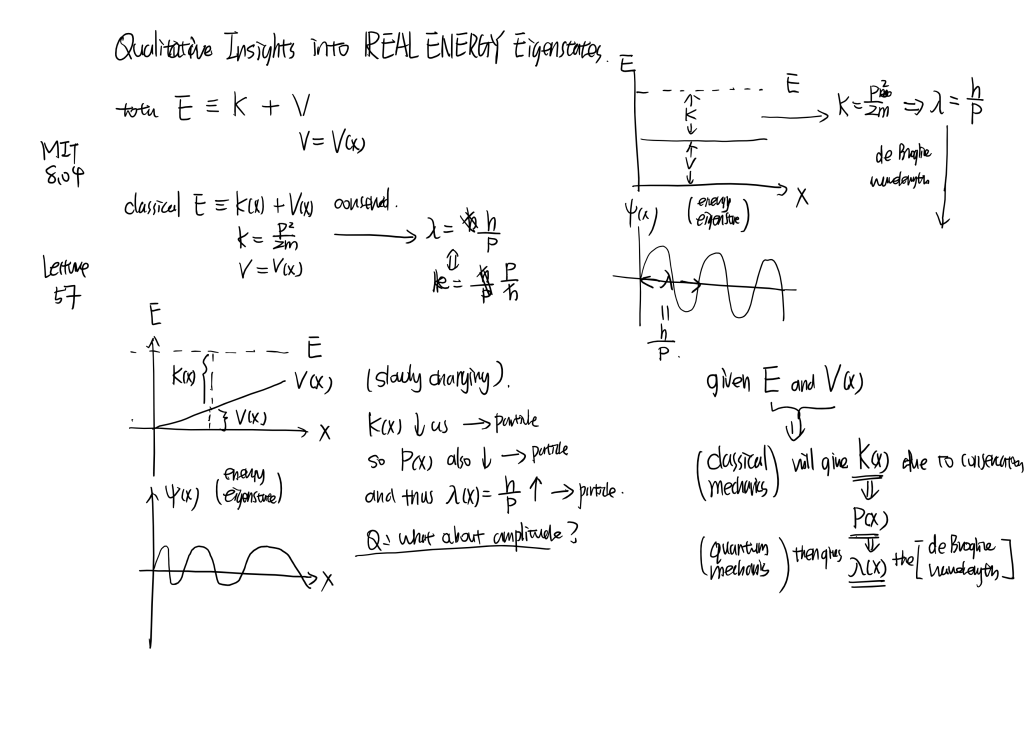
MIT8.04 [part14] Harmonic oscillator WCM0202下载 MIT 8.04 Complete Video link Guide page other notes
Read More
MIT8.04 [part15] Algebraic approach to simple harmonic oscillator WCM0213下载 MIT 8.04 Complete Video link Guide page other notes
Read More
MIT8.04 [part16] Scattering states and step potential section16下载 MIT 8.04 Complete Video link Guide page other notes
Read More
MIT 8.04 Complete Video link Guide page other notes
Read More
